题目内容
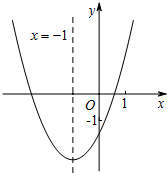 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=-1,与x轴的交点为(x1,0)、(x2,0),其中0<x1<1,有下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=-1,与x轴的交点为(x1,0)、(x2,0),其中0<x1<1,有下列结论:其中,正确的结论有( )
①abc>0;②-3<x2<-2;③4a+1>2b-c;④4ac-b2+4a<0;⑤a>
| 1 |
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:二次函数图象与系数的关系
专题:数形结合
分析:由抛物线开口方向得a>0,由抛物线的对称轴为直线x=-
=-1得b=2a>0,由抛物线与y轴的交点位置得c<0,则abc<0;由于抛物线与x轴一个交点在点(0,0)与点(1,0)之间,根据抛物线的对称轴性得到抛物线与x轴另一个交点在点(-3,0)与点(-2,0)之间,即有-3<x2<-2;由于b=2a,c<-1,则4a+1<2b-c;由于b=2a,则4ac-b2+4a=4a(a-c+1),再利用x=-1有a-b+c<0,则a-c>0,所以4ac-b2+4a=4a(a-c+1)>0;由于x=1时,函数为正值,则a+b+c>0,即a+2a+c>0,解得a>-
c,然后利用c<-1得到a>
.
| b |
| 2a |
| 1 |
| 3 |
| 1 |
| 3 |
解答:解:∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x=-
=-1,
∴b=2a>0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc<0,所以①错误;
∵抛物线y=ax2+bx+c与x轴一个交点在点(0,0)与点(1,0)之间,而对称轴为直线x=-1,
∴抛物线y=ax2+bx+c与x轴另一个交点在点(-3,0)与点(-2,0)之间,
∴-3<x2<-2,所以②正确;
∵b=2a,c<-1,
∴4a+1<2b-c,所以③错误;
∵b=2a,
∴4ac-b2+4a=4ac-4a2+4a=4a(a-c+1),
∵x=-1时,y<0,即a-b+c<0,
∴a-2a+c<0,即a-c>0,
∴4ac-b2+4a=4a(a-c+1)>0,所以④错误;
∵x=1时,y>0,即a+b+c>0,
∴a+2a+c>0,即a>-
c,
而c<-1,
∴a>
,所以⑤正确.
故选B.
∴a>0,
∵抛物线的对称轴为直线x=-
| b |
| 2a |
∴b=2a>0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc<0,所以①错误;
∵抛物线y=ax2+bx+c与x轴一个交点在点(0,0)与点(1,0)之间,而对称轴为直线x=-1,
∴抛物线y=ax2+bx+c与x轴另一个交点在点(-3,0)与点(-2,0)之间,
∴-3<x2<-2,所以②正确;
∵b=2a,c<-1,
∴4a+1<2b-c,所以③错误;
∵b=2a,
∴4ac-b2+4a=4ac-4a2+4a=4a(a-c+1),
∵x=-1时,y<0,即a-b+c<0,
∴a-2a+c<0,即a-c>0,
∴4ac-b2+4a=4a(a-c+1)>0,所以④错误;
∵x=1时,y>0,即a+b+c>0,
∴a+2a+c>0,即a>-
| 1 |
| 3 |
而c<-1,
∴a>
| 1 |
| 3 |
故选B.
点评:本题考查了二次函数的图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=-
;抛物线与y轴的交点坐标为(0,c);当b2-4ac>0,抛物线与x轴有两个交点;当b2-4ac=0,抛物线与x轴有一个交点;当b2-4ac<0,抛物线与x轴没有交点.
| b |
| 2a |

练习册系列答案
相关题目
 如图,D,E分别是△ABC的边AB,AC上的点,DE∥BC,若
如图,D,E分别是△ABC的边AB,AC上的点,DE∥BC,若| AD |
| DB |
| 2 |
| 3 |
| DE |
| BC |
A、
| ||
B、
| ||
C、
| ||
D、
|
对于二次函数y=-2(x+1)2+1,下列说法正确的是( )
| A、图象开口向上 |
| B、对称轴是直线x=1 |
| C、顶点坐标是(1,1) |
| D、函数y有最大值,且最大值是1 |
 化简并求值:
化简并求值: 如图,在△ABC中,点P是△ABC的外角∠DBC、∠BCE的平分线的交点,若∠BPC=70°,则∠BAC=
如图,在△ABC中,点P是△ABC的外角∠DBC、∠BCE的平分线的交点,若∠BPC=70°,则∠BAC=