题目内容
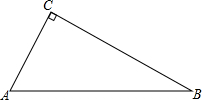 如图所示,在直角三角形ABC中,∠C=90°,AC=6,BC=8,将△ABC绕点B旋转90°,得到关于点A的对称点D,则AD的长是( )
如图所示,在直角三角形ABC中,∠C=90°,AC=6,BC=8,将△ABC绕点B旋转90°,得到关于点A的对称点D,则AD的长是( )| A、20 | ||
| B、10 | ||
C、10
| ||
D、20
|
考点:旋转的性质
专题:
分析:根据旋转的性质可得BD=AB,∠ABD=90°,然后判断出△ABD是等腰直角三角形,根据等腰直角三角形的斜边等于直角边的
倍解答即可.
| 2 |
解答:解:∵∠C=90°,AC=6,BC=8,
∴AB=
=
=10,
∵△ABC绕点B旋转90°得到关于点A的对称点D,
∴BD=AB,∠ABD=90°,
∴△ABD是等腰直角三角形,
∴AD=
AB=10
.
故选C.
∴AB=
| AC2+BC2 |
| 62+82 |
∵△ABC绕点B旋转90°得到关于点A的对称点D,
∴BD=AB,∠ABD=90°,
∴△ABD是等腰直角三角形,
∴AD=
| 2 |
| 2 |
故选C.
点评:本题考查了旋转的性质,等腰直角三角形的判定与性质,熟记性质并判断出△ABD是等腰直角三角形是解题的关键.

练习册系列答案
相关题目
对于二次函数y=-2(x+1)2+1,下列说法正确的是( )
| A、图象开口向上 |
| B、对称轴是直线x=1 |
| C、顶点坐标是(1,1) |
| D、函数y有最大值,且最大值是1 |
 如图,要在一面靠墙(墙长18米)的地方用30米长的不锈钢修建一个面积为100平方米的矩形花圃的护栏,问:围成的花圃的长和宽分别是多少?
如图,要在一面靠墙(墙长18米)的地方用30米长的不锈钢修建一个面积为100平方米的矩形花圃的护栏,问:围成的花圃的长和宽分别是多少?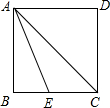 如图,已知:正方形ABCD中,∠BAC的平分线交BC于E,求证:AB+BE=AC.
如图,已知:正方形ABCD中,∠BAC的平分线交BC于E,求证:AB+BE=AC. 化简并求值:
化简并求值: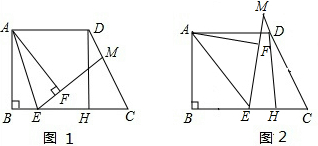
 如图,在△ABC中,点P是△ABC的外角∠DBC、∠BCE的平分线的交点,若∠BPC=70°,则∠BAC=
如图,在△ABC中,点P是△ABC的外角∠DBC、∠BCE的平分线的交点,若∠BPC=70°,则∠BAC=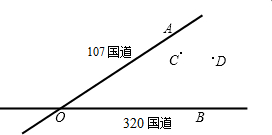 作图题,不写作方法但要保留作图痕迹
作图题,不写作方法但要保留作图痕迹