题目内容
在正方形ABCD中，P是BC边上与B、C不重合的任意点，DQ⊥AP于Q．证明：△DQA∽△ABP．考点：相似三角形的判定,正方形的性质
专题：证明题
分析：根据等角的余角相等求出∠BAP=∠QDA，再根据两组角对应相等，两三角形相似证明即可．
解答：证明：∵DQ⊥AP，
∴∠AQD=90°，
∴∠QDA+∠DAQ=90°，
在正方形ABCD中，∠BAD=∠B=90°，
∴∠BAP+∠DAQ=90°，
∴∠BAP=∠QDA，
又∵∠B=∠AQD=90°，
∴△DQA∽△ABP．
∴∠AQD=90°，
∴∠QDA+∠DAQ=90°，
在正方形ABCD中，∠BAD=∠B=90°，
∴∠BAP+∠DAQ=90°，
∴∠BAP=∠QDA，
又∵∠B=∠AQD=90°，
∴△DQA∽△ABP．
点评：本题考查了相似三角形的判定，正方形的性质，等角的余角相等的性质，熟记性质并求出∠BAP=∠QDA是解题的关键．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
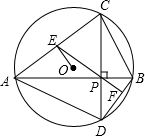如图，△ABC内接于⊙O，CD⊥AB于P，交⊙O于D，E为AC的中点，EP交BD于F，⊙O的直径为d．下列结论：
如图是一均匀薄板，半径R=30cm，现从板上挖掉一个r=15cm的内切圆，试求剩余薄板的重心C与大圆圆心O的距离．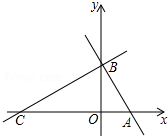
如图，平面直角坐标系中，直线l分别交x轴、y轴于A、B两点（OA＜OB）且OA、OB的长分别是一元二次方程x2-（