题目内容
11.计算:(1)(m-n)2+m(2n-m)+(m+n)(m-n)
(2)$\frac{1-x}{{x}^{2}+x}$÷(x-1-$\frac{2x-2}{x+1}$)-$\frac{1}{x}$.
分析 (1)原式利用完全平方公式,平方差公式,以及单项式乘以多项式法则计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,计算即可得到结果.
解答 解:(1)原式=m2-2mn+n2+2mn-m2+m2-n2=m2;
(2)原式=$\frac{1-x}{x(x+1)}$÷$\frac{{x}^{2}-2x+1}{x+1}$-$\frac{1}{x}$=-$\frac{x-1}{x(x+1)}$•$\frac{x+1}{(x-1)^{2}}$-$\frac{1}{x}$=-$\frac{1}{x(x-1)}$-$\frac{x-1}{x(x-1)}$=-$\frac{x}{x(x-1)}$=$\frac{1}{1-x}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19.某城市自来水收费实行阶梯水价,收费标准如表所示;某户5月份用水x吨(x>18),则交水费为多少元?若用水28吨,则水费为多少元?
| 月用水量 | 不超过12吨部分 | 超过12吨不超过18吨部分 | 超过18吨部分 |
| 收费标准(元/吨) | 2.00 | 2.50 | 3.00 |
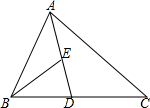 如图,AD是△ABC的中线,BE是△ABD的中线.
如图,AD是△ABC的中线,BE是△ABD的中线.
 如图,△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=152°,求∠A的度数.
如图,△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=152°,求∠A的度数.