题目内容
16.如图1,在△ABC中,∠C=90°,BC=8,AC=6,另有一直角梯形DEFH(HF∥DE,∠HDE=90°)的底边DE落在CB上,腰DH落在CA上,且DE=4,∠DEF=∠CBA,AH:AC=2:3.(1)延长HF交AB于G,求△AHG的面积.
(2)操作:固定△ABC,将直角梯形DEFH以每秒1个单位的速度沿CB方向向右移动,直到点D与点B重合时停止,设运动的时间为t秒,运动后的直角梯形为DEFH′(如图2).
探究1:在运动中,四边形CDH′H能否为正方形?若能,请求出此时t的值;若不能,请说明理由.
探究2:在运动过程中,延长HF交AB于G,三角形GEB能否为等腰三角形?若能,求出此时的t值;若不能,请说明理由.

分析 (1)由于三角形AHG和ACB相似,可通过相似比求出HG的值,然后根据三角形的面积计算公式即可求出三角形AHG的面积.
(2)①首先四边形CDH′H是个矩形,如果使四边形CDH′H成为正方形,那么需满足的条件是CD=DH′,可先根据AH:AC的值,求出HC的长即H′D的长,然后除以梯形的速度即可求出t的值.
②分三种情形,分别求解即可,注意t的取值范围;
解答 解:(1)∵AH:AC=2:3,AC=6
∴AH=$\frac{2}{3}$AC=$\frac{2}{3}$×6=4
又∵HF∥DE,
∴HG∥CB,
∴△AHG∽△ACB
∴$\frac{AH}{AC}$=$\frac{HG}{BC}$,
即 $\frac{4}{6}$=$\frac{HG}{8}$,
∴HG=$\frac{16}{3}$,
∴S△AHG=$\frac{1}{2}$AH•HG=$\frac{1}{2}$×4×$\frac{16}{3}$=$\frac{32}{3}$.
(2)①能为正方形
∵HH′∥CD,HC∥H′D,
∴四边形CDH′H为平行四边形,
又∠C=90°,
∴四边形CDH′H为矩形,
又CH=AC-AH=6-4=2
∴当CD=CH=2时,四边形CDH′H为正方形
此时可得t=2秒时,四边形CDH′H为正方形.
②如图,当BE1=BG时,∵BG=$\frac{10}{3}$,
∴此时t=(8-4-$\frac{10}{3}$)÷1=$\frac{2}{3}$s.
当E2G=E2B时,作E2M⊥AB于M.则BM=MG=$\frac{5}{3}$,
由△BME2∽△BCA,可得$\frac{BM}{BC}$=$\frac{B{E}_{2}}{AB}$,
∴BE2=$\frac{25}{12}$,
此时t=(8-4-$\frac{25}{12}$)÷1=$\frac{23}{12}$s.
当BG=BE3时,t=(8+$\frac{10}{3}$)÷1=$\frac{34}{3}$s.
∵t≤8,
∴此种情形不存在.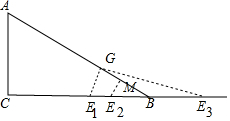
综上所述,满足条件的时间t的值为$\frac{2}{3}$S或$\frac{23}{12}$s.
点评 本题着重考查了图形平移变换、三角形相似的判定和性质、多边形的面积计算、分段函数、锐角三角函数等知识,解题的关键是灵活应用这些知识解决问题,学会分类讨论,不要漏解,属于中考压轴题.

(1)(m-n)2+m(2n-m)+(m+n)(m-n)
(2)$\frac{1-x}{{x}^{2}+x}$÷(x-1-$\frac{2x-2}{x+1}$)-$\frac{1}{x}$.
 如图,⊙O中,弦AB=2,点C在⊙O上,∠ACB=45°,则⊙O的半径等于( )
如图,⊙O中,弦AB=2,点C在⊙O上,∠ACB=45°,则⊙O的半径等于( )| A. | $\sqrt{2}$ | B. | 1 | C. | 2$\sqrt{2}$ | D. | 2 |
 如图,已知BE⊥AD,CF⊥AD,且BE=CF.
如图,已知BE⊥AD,CF⊥AD,且BE=CF. 已知二次函数顶点在x轴上,且过A(1,0),B(0,2)两点.
已知二次函数顶点在x轴上,且过A(1,0),B(0,2)两点. 已知:在Rt△ABD中,∠ABD=90°,以直角边AB为直径作圆O交AD于C,取线段BD的中点E,连接CE交AB的延长线于P.
已知:在Rt△ABD中,∠ABD=90°,以直角边AB为直径作圆O交AD于C,取线段BD的中点E,连接CE交AB的延长线于P.