题目内容
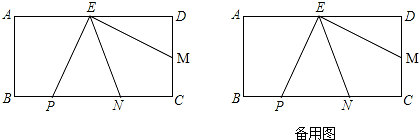
13.已知:矩形ABCD中,AD=2AB,E是AD中点,M为CD上的一点,PE⊥EM交CB于点P,EN平分∠PEM交BC于点N.(1)通过观察或测量BP与CM的长度,你能得到什么结论,不必证明;
(2)求证:BP2+CN2=PN2;
(3)过点P作PG⊥EN于点G,判断点G与△EDM的外接圆的位置关系?并说明理由.
分析 (1)利用已知利用刻度尺度量即可得出答案;
(2)利用全等三角形的判定与性质得出△BEP≌△CEM(ASA),进而得出△EPN≌△EMN(SAS),即可得出答案;
(3)首先判断出P、G、M三点共线,且G为PM的中点,然后利用直角三角形的性质得出GK=DK=EK=MK,即可得出答案.
解答  解:(1)结论:BP=CM;
解:(1)结论:BP=CM;
(2)证明:如图1,连接BE、CE,
∵四边形ABCD为矩形,AD=2AB,E为AD中点,
∴∠A=∠ABC=90°,AB=CD=AE=DE,
∴∠AEB=45°,∠DEC=45°,
在△ABE和△DCE中,
$\left\{\begin{array}{l}{AB=CD}\\{∠AEB=∠DEC}\\{AE=DE}\end{array}\right.$,
∴△ABE≌△DCE(SAS),∠BEC=90°,
∴BE=CE,
∴∠EBC=∠ECB=45°,
∴∠EBC=∠ECD,
又∵∠BEC=∠PEM=90°,
∴∠BEP=∠MEC,
在△BEP和△CEM中,
$\left\{\begin{array}{l}{∠EBP=∠ECM}\\{BE=CE}\\{∠BEP=∠CEM}\end{array}\right.$,
∴△BEP≌△CEM(ASA),
∴BP=MC,PE=ME,
∵EN平分∠PEM,
∴∠PEN=∠MEN=$\frac{1}{2}$=45°,
在△EPN和△EMN中,
$\left\{\begin{array}{l}{PE=ME}\\{∠PEN=∠MEN}\\{NE=NE}\end{array}\right.$,
∴△EPN≌△EMN(SAS),
∴PN=MN,
在Rt△MNC中有:MC2+NC2=MN2,
∴BP2+NC2=PN2.
(3)点G在△EDM的外接圆上,
理由:如图2,连接BE、CE、PM,
由(2),可得
PN=MN,PE=ME,
∴EN垂直平分PM,PG⊥EN,
∴P、G、M三点共线,且G为PM的中点,
∵K为EM中点,
∴GK=$\frac{1}{2}$ME,
又∵∠ADC=90°,
∴DK=$\frac{1}{2}$ME,
∴GK=DK=EK=MK,
∴点G在以K为圆心,DK为半径的圆上,即点G在△EDM的外接圆上.
点评 此题主要考查了四边形综合以及全等三角形的判定与性质以及直角三角形的性质等知识,根据题意得出△EPN≌△EMN进而结合勾股定理得出结论是解题关键.

| A. | 相切 | B. | 相离 | C. | 相切或相交 | D. | 相离或相切 |
 如图,在平面直角坐标系中,OA=OB=OC=8,过点A的直线AD交BC于点D,交y轴与点G,△ABD的面积为△ABC面积的$\frac{1}{4}$.
如图,在平面直角坐标系中,OA=OB=OC=8,过点A的直线AD交BC于点D,交y轴与点G,△ABD的面积为△ABC面积的$\frac{1}{4}$.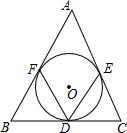 如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠B=60°,∠C=70°,求∠EDF的度数.
如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠B=60°,∠C=70°,求∠EDF的度数.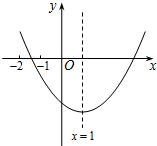 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2-4ac>0;②abc>0;③b=-2a;④9a+3b+c<0. 其中,正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2-4ac>0;②abc>0;③b=-2a;④9a+3b+c<0. 其中,正确结论的个数是( )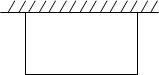 (1)如图,要搭建一个矩形的自行车棚,一边靠墙,另外三边围栏材料的总长为60m,怎样围才能使车棚的面积最大?
(1)如图,要搭建一个矩形的自行车棚,一边靠墙,另外三边围栏材料的总长为60m,怎样围才能使车棚的面积最大?