题目内容
17.已知在Rt△ABC中,∠C=90°,∠A=30°,E为直线AB上一点,且AE:EB=3:1,作EF垂直于直线AC,垂足为F,连接FB,则tan∠CFB的值等于$\frac{4\sqrt{3}}{3}$或$\frac{2\sqrt{3}}{3}$.分析 设BC=x,易得AC=$\sqrt{3}$x,进而根据平行线的性质,可分两种情况:①E在线段AB上时;②E在AB延长线上时;在Rt△BFC中,根据三角函数的定义计算.
解答 解:设BC=x,
∵在Rt△ABC中,∠C=90°,∠A=30°,
∴AC=$\sqrt{3}$x.
∵EF⊥AC,BC⊥AC,
∴EF∥BC.
分两种情况: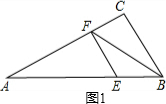 ①E在线段AB上时,如图1,
①E在线段AB上时,如图1,
∵EF∥BC,AE:EB=3:1,
∴AF:FC=AE:EB=3:1,
∴FC=$\frac{1}{4}$AC=$\frac{\sqrt{3}}{4}$x.
在Rt△BFC中,
tan∠CFB=$\frac{BC}{CF}$=$\frac{x}{\frac{\sqrt{3}}{4}x}$=$\frac{4\sqrt{3}}{3}$;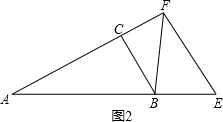 ②E在AB延长线上时,如图2,
②E在AB延长线上时,如图2,
∵EF∥BC,AE:EB=3:1,
∴AF:FC=AE:EB=3:1,
∴FC=$\frac{1}{2}$AC=$\frac{\sqrt{3}}{2}$x.
在Rt△BFC中,
tan∠CFB=$\frac{BC}{CF}$=$\frac{x}{\frac{\sqrt{3}}{2}x}$=$\frac{2\sqrt{3}}{3}$.
故答案为$\frac{4\sqrt{3}}{3}$或$\frac{2\sqrt{3}}{3}$.
点评 本题考查了解直角三角形,平行线的性质的运用,注意结合三角函数的定义解题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
8.下列说法不正确的是( )
| A. | 304.35是精确到百分位 | B. | 4.609万精确到万位 | ||
| C. | 6300是精确到个位 | D. | 近似数5.30和5.3的精确度不一样 |
12. 如图所示的格点图中,每相邻两点间的距离都相等,以图中的点为顶点,能画出的菱形有( )
如图所示的格点图中,每相邻两点间的距离都相等,以图中的点为顶点,能画出的菱形有( )
 如图所示的格点图中,每相邻两点间的距离都相等,以图中的点为顶点,能画出的菱形有( )
如图所示的格点图中,每相邻两点间的距离都相等,以图中的点为顶点,能画出的菱形有( )| A. | 3个 | B. | 6个 | C. | 9个 | D. | 18个 |
2.已知y是x的反比例函数,下表给出了x,y的一些值:
(1)写出这个反比例函数的解析式:
(2)根据表达式完成上表.
| x | -1 | -2 | 3 | 1 | 1 | 2 | -$\frac{1}{2}$ |
| y | 3 | $\frac{3}{2}$ | -1 | -3 | -3 | -$\frac{3}{2}$ | 6 |
(2)根据表达式完成上表.
9.把方程2(x-1)-3(1-x)=x,化成“ax=b”的形式为( )
| A. | 4x=5 | B. | -2x=5 | C. | 6x=5 | D. | 6x=1 |
7.要使$\frac{x+y}{xy}$有意义,则下列说法中正确的是( )
| A. | x、y全不为零 | B. | x=0或y=0 | C. | x、y不全为零 | D. | x、y全为零 |
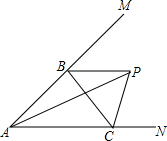 如图,点P在∠MAN内,点B,C分别是AM,AN上的点,∠MBC和∠NCB的平分线相交于点P.若∠APB=24°,则∠ACB的度数为48°.
如图,点P在∠MAN内,点B,C分别是AM,AN上的点,∠MBC和∠NCB的平分线相交于点P.若∠APB=24°,则∠ACB的度数为48°.