题目内容
7.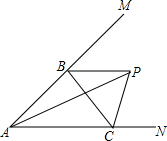 如图,点P在∠MAN内,点B,C分别是AM,AN上的点,∠MBC和∠NCB的平分线相交于点P.若∠APB=24°,则∠ACB的度数为48°.
如图,点P在∠MAN内,点B,C分别是AM,AN上的点,∠MBC和∠NCB的平分线相交于点P.若∠APB=24°,则∠ACB的度数为48°.
分析 过点P作PD⊥AM于D,PE⊥BC于E,PF⊥AN于F,根据角平分线上的点到角的两边的距离相等可得PD=PE,PE=PF,从而得到PD=PF,再根据到角的两边距离相等点在角的平分线上判断出AP平分∠MAN,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式整理可得∠ACB=2∠APB.
解答  解:如图,过点P作PD⊥AM于D,PE⊥BC于E,PF⊥AN于F,
解:如图,过点P作PD⊥AM于D,PE⊥BC于E,PF⊥AN于F,
∵BP、CP分别是∠MBC和∠NCB的平分线,
∴PD=PE,PE=PF,
∴PD=PF,
∴AP平分∠MAN,
∴∠BAP=$\frac{1}{2}$∠BAC,
在△ABC中,∠CBM=∠BAC+∠ACB,
在△ABP中,∠PBM=∠BAP+∠APB,
∵BP是∠MBC的平分线,
∴∠PBM=$\frac{1}{2}$∠CBM,
∴∠BAP+∠APB=$\frac{1}{2}$(∠BAC+∠ACB),
=$\frac{1}{2}$∠BAC+$\frac{1}{2}$∠ACB,
∴∠APB=$\frac{1}{2}$∠ACB,
∴∠ACB=2∠APB=2×24°=48°.
故答案为:48°.
点评 本题考查了角平分线上的点到角的两边的距离相等的性质,到角的两边距离相等点在角的平分线上的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并作出辅助线是解题的关键.

练习册系列答案
相关题目
19.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
那么下列判断中正确的是( )
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | -5 | 1 | 3 | 1 | … |
| A. | 该函数图象开口向上 | |
| B. | 该函数图象与y轴交于负半轴 | |
| C. | 当x=4时,y>0 | |
| D. | 方程y=ax2+bx+c=0的正跟在2和3之间 |
16.股民小王上星期买进某股票1000股,每股25元,下表为本周内每日该股票收盘价比前一天的涨跌情况(单位:元)
(1)星期四收盘时,每股是多少元?
(2)本周内最高价是每股多少元?最低价是每股多少元?
(3)已知买进股票是需付1.5‰的手续费,卖出时需付成交额的1.5‰的手续费和1‰的交易税,如果小王在先前五前将全部股票卖出,他的收盘情况如何?
| 星 期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌(元) | +4 | +4.5 | -1.5 | -2.5 | -6 |
(2)本周内最高价是每股多少元?最低价是每股多少元?
(3)已知买进股票是需付1.5‰的手续费,卖出时需付成交额的1.5‰的手续费和1‰的交易税,如果小王在先前五前将全部股票卖出,他的收盘情况如何?
 如图,在△ABC中,AB=AC=10,BC=12,D,E分别是边BC,AB的中点,AD平分EP,试判断以EP为直径的圆与直线AC的位置关系,并说明理由.
如图,在△ABC中,AB=AC=10,BC=12,D,E分别是边BC,AB的中点,AD平分EP,试判断以EP为直径的圆与直线AC的位置关系,并说明理由.