题目内容
10.如图,在△ABC中,∠ACB=90°,∠B=30°,AC=1,AC在直线l上.将△ABC绕点A顺时针旋转到位置①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+$\sqrt{3}$;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+$\sqrt{3}$;…,按此规律继续旋转,直到得到点P2016为止,则AP2016=( )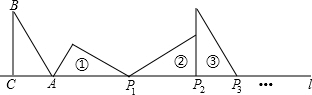
| A. | $2016+671\sqrt{3}$ | B. | $2015+672\sqrt{3}$ | C. | $2016+672\sqrt{3}$ | D. | $2015+671\sqrt{3}$ |
分析 观察不难发现,每旋转3次为一个循环组依次循环,用2016除以3求出循环组数,然后列式计算即可得解.
解答 解:由图可知,每旋转3次为一个循环组依次循环,
∵2016÷3=672,
∴AP2016正好为672个循环组的长度,
∵AP3=3+$\sqrt{3}$,
∴AP2016=672•AP3=672×(3+$\sqrt{3}$)=2016+672$\sqrt{3}$.
故选C.
点评 本题考查了旋转的性质,读懂题目信息并仔细观察图形得到每旋转3次为一个循环组依次循环是解题的关键.

练习册系列答案
相关题目
20.在函数y=$\frac{\sqrt{3-x}}{x+2}$中,自变量x的取值范围是( )
| A. | x≤3且x≠-2 | B. | x≤3 | C. | x≠-2 | D. | x<3且x≠-2 |
1. 如图,△ABC中,AB=AC,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,下列结论:①DE=DF;②DA平分∠EDF;③AE=AF;④AD上的点到AB、AC两边距离相等.其中正确的有( )
如图,△ABC中,AB=AC,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,下列结论:①DE=DF;②DA平分∠EDF;③AE=AF;④AD上的点到AB、AC两边距离相等.其中正确的有( )
 如图,△ABC中,AB=AC,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,下列结论:①DE=DF;②DA平分∠EDF;③AE=AF;④AD上的点到AB、AC两边距离相等.其中正确的有( )
如图,△ABC中,AB=AC,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,下列结论:①DE=DF;②DA平分∠EDF;③AE=AF;④AD上的点到AB、AC两边距离相等.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.为了帮助本市一名患病的高中生,某班15名同学积极捐款,他们捐款数额如表:
关于这15名同学所捐款的数额,下列说法正确的是( )
| 捐款的数额(单位:元) | 5 | 10 | 20 | 50 | 100 |
| 人数(单位:人) | 2 | 4 | 5 | 3 | 1 |
| A. | 众数是100 | B. | 中位数是30 | C. | 极差是20 | D. | 中位数是20 |
5.估计$\sqrt{19}$的值( )
| A. | 在2到3之间 | B. | 在3到4之间 | C. | 在4到5之间 | D. | 在5到6之间 |
15. 甲、乙两人进行羽毛球比赛,甲发出一个十分关键的球,出手点为P,羽毛球距地面高度h(米)与其飞行的水平距离s(米)之间的关系式为h=-$\frac{1}{12}$s2+$\frac{2}{3}$s+$\frac{3}{2}$.如图,已知球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为$\frac{9}{4}$米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是( )
甲、乙两人进行羽毛球比赛,甲发出一个十分关键的球,出手点为P,羽毛球距地面高度h(米)与其飞行的水平距离s(米)之间的关系式为h=-$\frac{1}{12}$s2+$\frac{2}{3}$s+$\frac{3}{2}$.如图,已知球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为$\frac{9}{4}$米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是( )
 甲、乙两人进行羽毛球比赛,甲发出一个十分关键的球,出手点为P,羽毛球距地面高度h(米)与其飞行的水平距离s(米)之间的关系式为h=-$\frac{1}{12}$s2+$\frac{2}{3}$s+$\frac{3}{2}$.如图,已知球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为$\frac{9}{4}$米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是( )
甲、乙两人进行羽毛球比赛,甲发出一个十分关键的球,出手点为P,羽毛球距地面高度h(米)与其飞行的水平距离s(米)之间的关系式为h=-$\frac{1}{12}$s2+$\frac{2}{3}$s+$\frac{3}{2}$.如图,已知球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为$\frac{9}{4}$米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是( )| A. | 4<m<8+$\sqrt{7}$ | B. | 4-$\sqrt{7}$<m<5 | C. | 5<m<9 | D. | 5<m<4+$\sqrt{7}$ |
2.实数x满足什么条件时,分式$\frac{1}{3-x}$有意义( )
| A. | x=3 | B. | x≠3 | C. | x<3 | D. | x>3 |
19.小王同时掷甲、乙两枚质地均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).记甲立方体朝上一面上的数字为x,乙立方体朝上一面上的数字为y,这样就确定点P的一个坐标(x,y),那么点P落在双曲线y=$\frac{4}{x}$上的概率为( )
| A. | $\frac{1}{18}$ | B. | $\frac{1}{10}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{6}$ |
20. 在数轴上表示有理数a、b的点的位置如图所示,那么下列各式成立的是( )
在数轴上表示有理数a、b的点的位置如图所示,那么下列各式成立的是( )
 在数轴上表示有理数a、b的点的位置如图所示,那么下列各式成立的是( )
在数轴上表示有理数a、b的点的位置如图所示,那么下列各式成立的是( )| A. | a>b | B. | -a<b | C. | -b>a | D. | |a|<|b| |