题目内容
16.先化简,再求值:$\frac{4({x}^{2}-x)}{x-1}$+(x-2)2-6$\sqrt{\frac{{x}^{2}}{9}}$,其中,x=$\sqrt{5}$+1.分析 原式第一项约分,第二项利用完全平方公式化简,第三项利用二次根式性质计算得到最简结果,把x的值代入计算即可求出值.
解答 解:∵x=$\sqrt{5}$+1>0,
∴原式=$\frac{4x(x-1)}{x-1}$+x2-4x+4-2x
=4x+x2-4x+4-2x
=x2-2x+4
=(x-1)2+3
=5+3
=8.
点评 此题考查了二次根式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
5.下列运算中正确的是( )
| A. | (ab2)3=ab6 | B. | (3xy)3=9x3y3 | C. | (-2a2)2=4a4 | D. | (ab)3=ab3 |
6.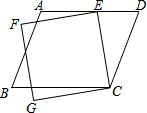 如图,已知?ABCD与正方形CEFG,其中E点在AD上.若∠ECD=35°,∠AEF=15°,则∠B的度数是( )
如图,已知?ABCD与正方形CEFG,其中E点在AD上.若∠ECD=35°,∠AEF=15°,则∠B的度数是( )
 如图,已知?ABCD与正方形CEFG,其中E点在AD上.若∠ECD=35°,∠AEF=15°,则∠B的度数是( )
如图,已知?ABCD与正方形CEFG,其中E点在AD上.若∠ECD=35°,∠AEF=15°,则∠B的度数是( )| A. | 75° | B. | 70° | C. | 55° | D. | 50° |
 如图,在?ABCD中,BD为对角线,E、F是BD上的点,且BE=DF.
如图,在?ABCD中,BD为对角线,E、F是BD上的点,且BE=DF.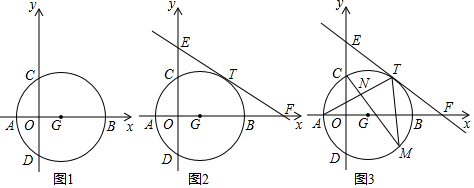
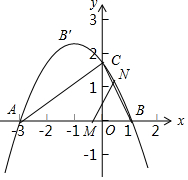 如图,已知点A(-3,0),二次函数y=ax2+bx+$\sqrt{3}$的对称轴为直线x=-1,其图象过点A与x轴交于另一点B,与y轴交于点C.
如图,已知点A(-3,0),二次函数y=ax2+bx+$\sqrt{3}$的对称轴为直线x=-1,其图象过点A与x轴交于另一点B,与y轴交于点C.