题目内容
 如图,正方形ABCD的边长为2,点E是BC边上一点,EF⊥AE交CD于点F,设BE=x,CF=y,则下列表示y关于x的函数图象中正确的是( )
如图,正方形ABCD的边长为2,点E是BC边上一点,EF⊥AE交CD于点F,设BE=x,CF=y,则下列表示y关于x的函数图象中正确的是( )A、 |
B、 |
C、 |
D、 |
考点:动点问题的函数图象
专题:
分析:通过设出BE=x,FC=y,且△AEF为直角三角形,运用勾股定理得出y与x的关系,在判断出函数图象.
解答: 解:如图,连接AF.
解:如图,连接AF.
设BE=x,FC=y,则AE2=x2+22,EF2=(2-x)2+y2,AF2=(2-y)2+22.
又∵△AEF为直角三角形,
∴AE2+EF2=AF2.即x2+22+(2-x)2+y2=(2-y)2+22
整理 得y=-
x2+x=-
(x-1)2+0.5.
该函数图象是开口向下、顶点坐标是(1,0.5)的抛物线.
很明显,函数对应A选项.
故选:A.
 解:如图,连接AF.
解:如图,连接AF.设BE=x,FC=y,则AE2=x2+22,EF2=(2-x)2+y2,AF2=(2-y)2+22.
又∵△AEF为直角三角形,
∴AE2+EF2=AF2.即x2+22+(2-x)2+y2=(2-y)2+22
整理 得y=-
| 1 |
| 2 |
| 1 |
| 2 |
该函数图象是开口向下、顶点坐标是(1,0.5)的抛物线.
很明显,函数对应A选项.
故选:A.
点评:此题考查了动点问题的函数图象,关键列出动点的函数关系,再判断选项.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
在直角坐标系中,已知A(1,O),B(3,3),C(0,2),则△ABC的三边长a,b,c的大小关系是( )
| A、a<b<c |
| B、c<a<b |
| C、c<b<a |
| D、b<a<c |
| 2 |
| 3 |
| A、m=2 | ||
B、m=
| ||
C、m=
| ||
| D、无法确定 |
下列函数中,y随x的增大而增大的是( )
A、y=-
| ||
B、y=
| ||
| C、y=-2x+4 | ||
| D、y=-2(x-3)2-1(x<1) |
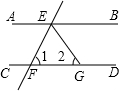 如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF.若∠1=72°,则∠2的度数为( )
如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF.若∠1=72°,则∠2的度数为( )| A、36° | B、54° |
| C、45° | D、68° |
下列二次根式中,能与
合并的式子的是( )
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图所示,在矩形ABCD中,AD=10,DC=8,点E为AB边上一点,△BCE沿EC所在直线翻折,使得B点刚好落在AD边上F处.
如图所示,在矩形ABCD中,AD=10,DC=8,点E为AB边上一点,△BCE沿EC所在直线翻折,使得B点刚好落在AD边上F处. 已知如图,?ABCD,连结AC,
已知如图,?ABCD,连结AC,