题目内容
5. 已知,如图,在四边形ABCD中,BC>BA,∠A+∠C=180°,DE⊥BC,BD平分∠ABC,试说明AD=DC.
已知,如图,在四边形ABCD中,BC>BA,∠A+∠C=180°,DE⊥BC,BD平分∠ABC,试说明AD=DC.
分析 过D作DF⊥AB,交BA的延长线于点F,由角平分线的性质可知DE=DF,则可证明△ADF≌△CDE,可证明AD=DC.
解答  证明:
证明:
如图,过D作DF⊥AB,交BA的延长线于点F,
∵DE⊥BC,BD平分∠ABC,
∴DE=DF,∠F=∠DEC=90°,
∵∠BAD+∠C=180°,且∠BAD+∠DAF=180°,
∴∠DAF=∠C,
在△ADF和△CDE中
$\left\{\begin{array}{l}{∠DAF=∠C}\\{∠F=∠DEC}\\{DF=DE}\end{array}\right.$
∴△ADF≌△CDE(AAS),
∴AD=CD.
点评 本题主要考查全等三角形的判定和性质,构造全等三角形利用角平分线的性质证得全等是解题的关键.

练习册系列答案
相关题目
20.定义一种运算:ak=ak-1+1-5([$\frac{k-1}{5}$]-[$\frac{k-2}{5}$]),其中k是正整数,且k?2,[x]表示非负实数x的整数部分,例如[2.6]=2,[0.8]=0.若a1=1,则a2016的值为( )
| A. | 2017 | B. | 1 | C. | 2016 | D. | 2 |
10.李庄与张庄两地之间的距离是100千米,若汽车以平均每小时80千米的速度从李庄开往张庄,则汽车距张庄的路程y(千米)与行驶时间x(小时)之间的函数关系式是( )
| A. | y=80x-100 | B. | y=-80x-100 | C. | y=80x+100 | D. | y=-80x+100 |
 请找出图中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有5个.
请找出图中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有5个. 在△ABC中,AP为∠A的平分线,AM为BC边上的中线,过B作BH⊥AP于H,AM的延长线交BH于Q,求证:PQ∥AB.
在△ABC中,AP为∠A的平分线,AM为BC边上的中线,过B作BH⊥AP于H,AM的延长线交BH于Q,求证:PQ∥AB.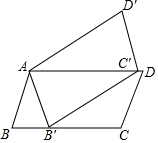 如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点),点B′恰好落在BC边上,则∠C=105°.
如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点),点B′恰好落在BC边上,则∠C=105°.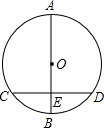 如图,⊙O直径AB垂直于弦CD,垂足E是OB的中点,若AB=6,则CD=3$\sqrt{3}$.
如图,⊙O直径AB垂直于弦CD,垂足E是OB的中点,若AB=6,则CD=3$\sqrt{3}$.