题目内容
14. 如图,这是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为4m的半圆,其边缘AB=CD=18m,点E在CD上,CE=2cm,一滑行爱好者从A点到E点,再从E点滑行到B点,则他滑行的最短距离是多少?(边缘部分的厚度可以忽略不计,π取3)
如图,这是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为4m的半圆,其边缘AB=CD=18m,点E在CD上,CE=2cm,一滑行爱好者从A点到E点,再从E点滑行到B点,则他滑行的最短距离是多少?(边缘部分的厚度可以忽略不计,π取3)
分析 要求滑行的最短距离,需将该U型池的侧面展开,进而根据“两点之间线段最短”得出结果.
解答  解:其侧面展开图如图:AD=BC=πR=4π=12,AB=CD=18m,DE=CD-CE=18-2=16m,
解:其侧面展开图如图:AD=BC=πR=4π=12,AB=CD=18m,DE=CD-CE=18-2=16m,
在Rt△ADE中,AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=20(m),
在Rt△BCE中,BE=$\sqrt{C{E}^{2}+B{C}^{2}}$=2$\sqrt{37}$(m),
AE+BE=20+2$\sqrt{37}$(m).
故他滑行的最短距离是(20+2$\sqrt{37}$)m.
点评 考查了平面展开-最短路径问题,U型池的侧面展开图是一个矩形,此矩形的宽等于半径为4m的半圆的弧长,矩形的长等于AB=CD=18m.本题就是把U型池的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
6.将平面直角坐标系中的点P(-2,3),绕坐标原点O顺时针旋转90°,到达点P′,则点P′的坐标是( )
| A. | (2,3) | B. | (2,-3) | C. | (-3,-2) | D. | (3,2) |
 函数图象有一个公共点,我们就称两个函数图象“共一点”,有两个公共点,则称它们“共两点”…
函数图象有一个公共点,我们就称两个函数图象“共一点”,有两个公共点,则称它们“共两点”…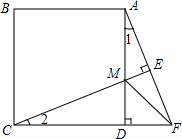 已知,如图在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M,求证:∠MFD=45°.
已知,如图在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M,求证:∠MFD=45°.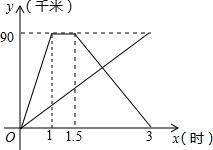 甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑电动车,甲到达B地停留半个小时后返回A地,如图是他们离A地的距离y(千米)与经过的时间x(小时)之间的函数关系图象.
甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑电动车,甲到达B地停留半个小时后返回A地,如图是他们离A地的距离y(千米)与经过的时间x(小时)之间的函数关系图象.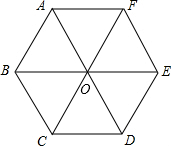 如图,正六边形ABCDEF是由边长为2厘米的六个等边三角形拼成,那么图中
如图,正六边形ABCDEF是由边长为2厘米的六个等边三角形拼成,那么图中
 作图题:作出四边形ABCD关于O点成中心对称的四边形AˊBˊCˊDˊ.
作图题:作出四边形ABCD关于O点成中心对称的四边形AˊBˊCˊDˊ.