题目内容
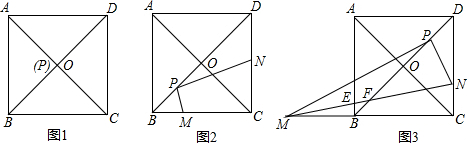
7.已知:如图,正方形ABCD中,边长为4,对角线AC、BD交于点O,P是线段BD上一动点,PM⊥PN分别交直线BC、CD于M、N.(1)如图1,点P和O重合时,求证:PM=PN;
(2)如图2,点P为线段OB的中点时,求证:BM+$\frac{1}{3}$DN=2;
(3)如图3,点P为线段OD的中点时,且CN=$\frac{1}{3}$DN,连接MN分别交AB、BD于E、F,直接写出线段EF的长.
分析 (1)根据∠MPC=∠NPD,CP=DP,∠PCM=∠PDN=45°,判定△PCM≌△PDN,根据全等三角形的对应边相等,即可得出PM=PN;
(2)过P作PQ⊥BD,交BC于Q,判定△MPQ∽△NPD,得到$\frac{MQ}{ND}$=$\frac{PQ}{PD}$,根据MQ=$\frac{1}{3}$DN,BQ=$\frac{1}{2}$BC=2,即可得出BM+$\frac{1}{3}$DN=2;
(3)过P作PQ⊥BD,交CD于Q,判定△PBM∽△PQN,得到$\frac{NQ}{MB}$=$\frac{PQ}{PB}$,根据BM=3NQ,求得CN,BM,ME以及EN的长,再根据△MBE∽△MCN,△BEF∽△DNF,即可得出EN的长,根据相似三角形的性质得到线段EF的长.
解答 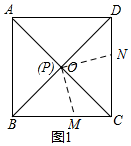 解:(1)依题意得,∠MPN=∠CPD=90°,
解:(1)依题意得,∠MPN=∠CPD=90°,
∴∠MPC=∠NPD,
又∵正方形ABCD中,AC、BD交于点O,
∴CP=DP,∠PCM=∠PDN=45°,
在△PCM和△PDN中,
$\left\{\begin{array}{l}{∠MPC=∠NPD}\\{CP=DP}\\{∠PCM=∠PDN}\end{array}\right.$,
∴△PCM≌△PDN(ASA),
∴PM=PN;
(2)证明:如图2,过P作PQ⊥BD,交BC于Q,则∠BPQ=90°,
∴∠PQM=∠PDN=45°,
依题意得,∠MPN=∠QPD=90°,
∴∠MPQ=∠NPD,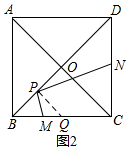
∴△MPQ∽△NPD,
∴$\frac{MQ}{ND}$=$\frac{PQ}{PD}$,
∵点P为线段OB的中点,
∴BP=$\frac{1}{2}$BO=$\frac{1}{2}$OD,即BP=$\frac{1}{3}$PD,
∴PQ=$\frac{1}{3}$PD,
∴$\frac{MQ}{ND}$=$\frac{1}{3}$,即MQ=$\frac{1}{3}$DN,
∵PQ∥OC,点P为线段OB的中点,
∴点Q为BC的中点,
∴BQ=$\frac{1}{2}$BC=2,即BM+MQ=2,
∴BM+$\frac{1}{3}$DN=2;
(3)EF=$\frac{5}{14}\sqrt{2}$.
理由:如图3,过P作PQ⊥BD,交CD于Q,则∠BPQ=∠MPN=90°,∠PQD=45°,
∴∠MPB=∠NPQ,
∵∠PQD=∠PBC=45°,
∴∠PBM=∠PQN=135°,
∴△PBM∽△PQN,
∴$\frac{NQ}{MB}$=$\frac{PQ}{PB}$,
又∵点P为线段OD的中点,
∴PD=$\frac{1}{3}$PB=PQ,
∴$\frac{NQ}{MB}$=$\frac{1}{3}$,即BM=3NQ,
∵CN=$\frac{1}{3}$DN=$\frac{1}{4}$CD=1,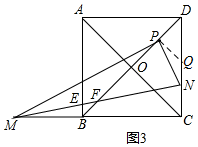
∴DN=3,
∵PQ∥OC,P为线段OD的中点,
∴Q为CD的中点,
∴DQ=$\frac{1}{2}$CD=2,
∴NQ=3-2=1,
∴BM=3NQ=3,CM=3+4=7,
∴Rt△CMN中,MN=$\sqrt{{7}^{2}+{1}^{2}}$=5$\sqrt{2}$,
∵EB∥NC,
∴△MBE∽△MCN,△BEF∽△DNF,
∴$\frac{BE}{CN}$=$\frac{MB}{MC}$=$\frac{ME}{MN}$,即$\frac{BE}{1}$=$\frac{3}{7}$=$\frac{ME}{5\sqrt{2}}$,
∴BE=$\frac{3}{7}$,ME=$\frac{15}{7}\sqrt{2}$,
∴EN=MN-ME=5$\sqrt{2}$-$\frac{15}{7}\sqrt{2}$=$\frac{20}{7}\sqrt{2}$,
∵$\frac{EF}{NF}=\frac{BE}{DN}$,
∴$\frac{EF}{\frac{20}{7}\sqrt{2}-EF}$=$\frac{\frac{3}{7}}{3}$,
解得EF=$\frac{5}{14}\sqrt{2}$.
点评 本题属于四边形综合题,主要考查了相似三角形的判定与性质,正方形的性质,勾股定理以及全等三角形的判定与性质的综合应用,解决问题的关键是作辅助线构造全等三角形以及相似三角形,利用相似三角形的对应边成比例得到线段的长.

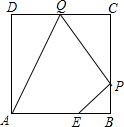 如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是$\frac{9}{2}$.
如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是$\frac{9}{2}$. | 产品 | A | B |
| 进价 | 3000元/千克 | 4000元/千克 |
| 售价 | 4150元/千克 | 5500元/千克 |
(2)若该经销商在销售结束时将剩余的10%的A种产品和20%的B种产品交回厂家,求他在这次销售中获利多少元?
(3)若该经销商计划再次购进这两种产品共100千克,假设还会有10%的A产品和20%的B产品不能售出要交回厂家,求本次该经销商购进A、B两种产品各多少千克时可在销售中获利89890元?

 如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.在AB边上有一个动点F,且不与点A,B重合.当AF=$\frac{16}{11}$时,△MEF的周长最小.
如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.在AB边上有一个动点F,且不与点A,B重合.当AF=$\frac{16}{11}$时,△MEF的周长最小.