Question

15．如图，在矩形纸片ABCD中，AB=4，AD=12，将矩形纸片折叠，使点C落在AD边上的点M处，折痕为PE，此时PD=3．在AB边上有一个动点F，且不与点A，B重合．当AF=$\frac{16}{11}$时，△MEF的周长最小．

Answer 1

分析 如图1，做点M关于AB的对称点M′，连接M′E交AB于点F，则点F即为所求，过点E作EN⊥AD，垂足为N，由（1）可得AM，利用勾股定理可得ME和NM′，由△AFM′∽△NEM′，利用相似三角形的性质可得AF；

解答 解：∵四边形ABCD为矩形，
∴CD=AB=4，∠D=90°，
∵矩形ABCD折叠，使点C落在AD边上的点M处，折痕为PE，
∴PD=PH=3，CD=MH=4，∠H=∠D=90°，
∴PM=5，
如图1，做点M关于AB的对称点M′，连接M′E交AB于点F，则点F即为所求，过点E作EN⊥AD，垂足为N，
∵AM=AD-MP-PD=12-5-3=4，
∴AM=AM′=4，
∵矩形ABCD折叠，使点C落在AD边上的点M处，折痕为PE，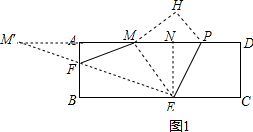
∴∠CEP=∠MEP，∠CEP=∠MPE，
∴∠MEP=∠MPE，
∴ME=MP=5；
在Rt△ENM中，MN=3，
∴NM′=11，
∵AF∥ME，
∴△AFM′∽△NEM′，
∴$\frac{M′A}{M′N}$=$\frac{AF}{EN}$，
即$\frac{4}{11}$=$\frac{AF}{4}$，
解得：AF=$\frac{16}{11}$，
即AF=$\frac{16}{11}$时，△MEF的周长最小；
故答案为：$\frac{16}{11}$．

点评 本题主要考查了折叠的性质和最短路径问题，做对称点利用勾股定理是解答此题的关键．