题目内容
13．商店将进价为每斤8元的草莓按每斤10元出售，每天可销售300斤，已知这种草莓每斤的售价每提高1元，销售量就会减少20斤，商店要确保每天销售草莓的利润达到1400元，且销售量不超过180斤，每斤草莓应提高多少元？分析 等量关系为：（原来每斤草莓的利润+提高的价格）×（原来的销售量-20×提高的价格）=1400，把相关数值代入计算即可．
解答 解：设每斤草莓应提高x元，根据题意可得：
（10-8+x）（300-20x）=1400，
解得：x1=5，x2=8，
当x=5时，300-20x=200＞180，所以x=5舍去；
当x=8时，300-20x=140＜180，所以x=8；
答：每斤草莓应提高8元．
点评 此题主要考查了一元二次方程的应用；根据利润得到相应的等量关系是解决本题的关键；得到销售量是解决本题的难点．
练习册系列答案
相关题目
3．
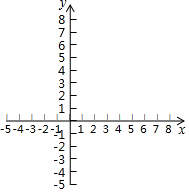数学李老师给学生出了这样一个问题：探究函数y=$\frac{x}{x+1}$的图象与性质，小斌根据学习函数的经验，对函数y=$\frac{x}{x+1}$的图象与性质进行了探究．下面是小斌的探究过程，请您补充完成：
（1）函数y=$\frac{x}{x+1}$的自变量x的取值范围是：x≠-1
（2）列出y与x的几组对应值，请直接写出m的值，m=3．
（3）请在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，并画出该函数的图象；
（4）结合函数的图象，写出函数y=$\frac{x}{x+1}$的一条性质．
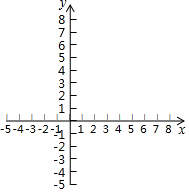数学李老师给学生出了这样一个问题：探究函数y=$\frac{x}{x+1}$的图象与性质，小斌根据学习函数的经验，对函数y=$\frac{x}{x+1}$的图象与性质进行了探究．下面是小斌的探究过程，请您补充完成：（1）函数y=$\frac{x}{x+1}$的自变量x的取值范围是：x≠-1
（2）列出y与x的几组对应值，请直接写出m的值，m=3．
| x | … | -5 | -4 | -3 | -2 | -$\frac{3}{2}$ | -$\frac{1}{2}$ | 0 | 1 | 2 | m | 4 | 5 | … |
| y | … | $\frac{5}{4}$ | $\frac{4}{3}$ | $\frac{3}{2}$ | 2 | 3 | -1 | 0 | $\frac{1}{2}$ | $\frac{2}{3}$ | $\frac{3}{4}$ | $\frac{4}{5}$ | $\frac{5}{6}$ | … |
（4）结合函数的图象，写出函数y=$\frac{x}{x+1}$的一条性质．
如图，已知AB∥CF，DE∥CF，DE与BC交于点P，若∠ABC=70°，∠CDE=130°．
8．已知a，b是方程x2+3x-1=0的两个实数根，则-$\frac{1}{a}$-$\frac{1}{b}$的值是（ ）
| A． | -3 | B． | -$\frac{1}{3}$ | C． | 3 | D． | $\frac{1}{3}$ |
已知：如图，在△ABC中，直线PQ垂直平分AC，与边AB交于点E，连接CE，过点C作CF∥BA交PQ于点F，连接AF．
如图，二次函数y=ax2+bx-4$\sqrt{3}$的图象经过A（-1，0）、B（4，0）两点，于y轴交于点D．