��Ŀ����
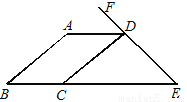
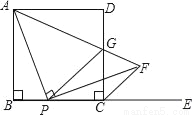
��ͼ����������ABCD�У�AB=a��PΪ��BC��һ���㣨����B��C�غϣ���E�DZ�BC�ӳ�����һ�㣬����AP������P��PF��AP����DCE��ƽ�����ڵ�F������AF���CD���ڵ�G������PG��
���룺�߶�PA��PF��������ϵΪ�� ����
̽������CPG���ܳ��ڵ�P���˶����Ƿ�ı䣿�����ı�����ֵ��
Ӧ�ã���PG��CF����a=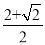 ʱ����PB=�� ����
ʱ����PB=�� ����
��ϰ��ϵ�д�
�����Ŀ