题目内容
19.已知⊙O中弦AB⊥弦CD于E,tan∠ACD=$\frac{3}{2}$(1)如图1,若AB为⊙O的直径,BE=8,求AC的长
(2)如图2,若AB不为⊙O的直径,BE=4,F为弧BC上一点,弧BF=弧BD,且CF=7,求AC的长.
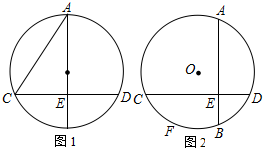
分析 (1)连接BD,根据垂径定理求得CE=DE,根据圆周角定理得出∠ACD=∠ABD,从而得出$\frac{ED}{EB}$=$\frac{AE}{CE}$=$\frac{3}{2}$,即$\frac{ED}{8}$=$\frac{3}{2}$,求得CE=ED=12,根据tan∠ACD=$\frac{3}{2}$,求得AE=$\frac{3}{2}$CE=18,然后应用勾股定理即可求得AC.
(2)连接CB,过B作BG⊥CF于G,由弧BF=弧BD,得出∠BCE=∠BCG,根据AAS证得△CEB≌△CGB,从而求得BG=BE=4,CE=CG,根据圆内接四边形的性质得出∠BFG=∠A,从而求得△BFG∽△CAE,根据相似三角形对应边成比例得出$\frac{FG}{BG}$=$\frac{AE}{CE}$=$\frac{3}{2}$,求得FB=$\frac{3}{2}$BG=6,进而求得CE=CG=13,然后根据勾股定理即可求得AC的长.
解答  解:(1)如图1,连接BD,
解:(1)如图1,连接BD,
∵直径AB⊥弦CD,
∴CE=DE,
∵∠ACD=∠ABD,
∴tan∠ABD=tan∠ACD=$\frac{3}{2}$,
∴$\frac{ED}{EB}$=$\frac{AE}{CE}$=$\frac{3}{2}$,即$\frac{ED}{8}$=$\frac{3}{2}$,
∴ED=12,
∴CE=ED=12,
∴AE=$\frac{3}{2}$CE=18,
∴AC=$\sqrt{A{E}^{2}+C{E}^{2}}$=6$\sqrt{13}$.
(2)连接CB,过B作BG⊥CF于G,
∵弧BF=弧BD,
∴∠BCE=∠BCG,
在△CEB和△CGB中
$\left\{\begin{array}{l}{∠BCE=∠BCG}\\{∠BEC=∠BGC}\\{BC=BC}\end{array}\right.$
∴△CEB≌△CGB(AAS),
∴BG=BE=4,
∵∠BFG=∠A,∠FGB=∠AEC=90°,
∴△BFG∽△CAE,
∴$\frac{FG}{BG}$=$\frac{AE}{CE}$=$\frac{3}{2}$,
∴FG=$\frac{3}{2}$BG=6,
∴CE=CG=13,
∴AC=$\frac{13}{2}$$\sqrt{13}$.
点评 本题考查了垂径定理、圆周角定理、圆内接四边形的性质、全等三角形的判定和性质,相似三角形的判定和性质、勾股定理的应用,(2)作出辅助线关键全等三角形是解题的关键.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案 如图①,是小明把一个梯形图沿对称轴剪开拼成图②,其中a>b.则由图①到图②能验证的公式是( )
如图①,是小明把一个梯形图沿对称轴剪开拼成图②,其中a>b.则由图①到图②能验证的公式是( )| A. | (a+b)(a-b)=a2-b2 | B. | a2-b2=(a-b)(a+b) | C. | (a-b)2=a2-2ab+b2 | D. | a2-2ab+b2=(a-b)2 |
| A. | 0.12×109元 | B. | 1.2×108元 | C. | 1.2×107元 | D. | 0.12×108元 |
| A. | $\sqrt{4}$=2 | B. | (-3)2=-9 | C. | 2-3=-6 | D. | 20=0 |
| A. | 2a2+a2=3a4 | B. | $\sqrt{{a}^{2}}$=a | C. | $\sqrt{8}$•$\sqrt{2}$=4 | D. | 2a2÷a2=2a |
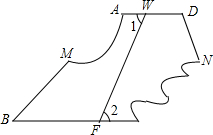 如图是一张四边形纸片ABCD被撕掉∠A和∠C后的剩余部分(∠A在左上角),量得∠1=∠2,∠B=45°,∠D=105°,在图中画出被撕掉的部分,并求原来∠A和∠C的度数.
如图是一张四边形纸片ABCD被撕掉∠A和∠C后的剩余部分(∠A在左上角),量得∠1=∠2,∠B=45°,∠D=105°,在图中画出被撕掉的部分,并求原来∠A和∠C的度数. 如图,O为矩形ABCD内的一点,且满足OB=OD,若O点到A点的距离用m表示,OB=n,试用含m、n的代数式表示OC=$\sqrt{2{n}^{2}-{m}^{2}}$.
如图,O为矩形ABCD内的一点,且满足OB=OD,若O点到A点的距离用m表示,OB=n,试用含m、n的代数式表示OC=$\sqrt{2{n}^{2}-{m}^{2}}$.