题目内容
5.甲、乙两个蔬菜基地,分别向A、B、C三个农贸市场提供同品种蔬菜,按签订的合同规定向A提供45t,向B提供75t,向C提供40t.甲基地可安排60t,乙基地可安排100t.甲、乙与A、B、C的距离千米数如下表所示,设运费为1元/(km•t).问如何安排使总运费最低?求出最小的总运费值.| A | B | C | |
| 甲 | 10 | 5 | 6 |
| 乙 | 4 | 8 | 15 |
分析 根据题中表格信息,可以先设乙基地向A提供xt,向B提供yt,根据关系可以得甲、乙两个蔬菜基地,分别向A、B、C三个农贸市场提供同品种蔬菜的吨数,然后列出式子,根据x和y的取值范围得出答案.
解答 解:设甲蔬菜基地分别向A、B两个农贸市场提供蔬菜x、y吨,则调运量如下表,总运费为w(元),
| A | B | C | |
| 甲(单位:吨) | x | y | 60-x-y |
| 乙(单位:吨) | 45-x | 75-y | x+y-20 |
化简得w=15x+6y+840=9x+6(x+y)+840,
∵$\left\{\begin{array}{l}x≥0\\ y≥0\\ 60-x-y≥0\\ 45-x≥0\\ 75-y≥0\\ x+y-20≥0\end{array}\right.$,
∴$\left\{\begin{array}{l}0≤x≤45\\ 0≤y≤75\\ 20≤x+y≤60\end{array}\right.$,
当x、x+y同时取最小值时,w取最小值,即x=0,x+y=20(此时y=20)时,w取最小值960元,
故调运方案为
| A | B | C | |
| 甲(单位:吨) | 0 | 20 | 40 |
| 乙(单位:吨) | 45 | 55 | 0 |
点评 本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题.注意利用一次函数求最值时,关键是应用一次函数的性质;即由函数y随x的变化,结合自变量的取值范围确定最值.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
13.如果向东走20m记作+20m,那么-30m表示( )
| A. | 向东走30m | B. | 向西走30m | C. | 向南走30m | D. | 向北走30m |
10.下列说法中正确的是( )
| A. | “打开电视,正在播放《新闻联播》”是必然事件 | |
| B. | 在两个等圆中,相等的圆心角所对的弧相等,所对的弦也相等 | |
| C. | 数据1,1,2,2,3的中位数为2,极差为2,众数也为2 | |
| D. | 一组数据的方差越小,这组数据波动越大 |
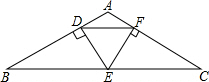 如图,△DEF是等边三角形,BC过点E,且平行于DF,又AB⊥ED,AC⊥EF,D,F是垂足.
如图,△DEF是等边三角形,BC过点E,且平行于DF,又AB⊥ED,AC⊥EF,D,F是垂足.