题目内容
17.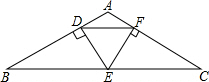 如图,△DEF是等边三角形,BC过点E,且平行于DF,又AB⊥ED,AC⊥EF,D,F是垂足.
如图,△DEF是等边三角形,BC过点E,且平行于DF,又AB⊥ED,AC⊥EF,D,F是垂足.(1)指出该图中有哪些等腰三角形(△DEF除外),并说明理由.
(2)若△DEF的边长为3,求△ABC的周长.
分析 (1)△ABC,△ADF是等腰三角形,由△DEF是等边三角形,得到∠EDF=∠EFD=60°,根据平行线的性质得到∠BED=∠EDF=60°,∠CEF=∠DFE=60°,由于AB⊥ED,AC⊥EF,得到∠B=∠C=30°,于是得到结果;
(2)由△DEF的边长为3,得到DE=EF=3,在Rt△BDE与Rt△CEF中,求得BE=CE=6,连接AE,则AE⊥BC,得到AB=AC=$\frac{\sqrt{3}}{2}$BE=3$\sqrt{3}$,即可得到结果.
解答 解:(1)△ABC,△ADF是等腰三角形,
理由:∵△DEF是等边三角形,
∴∠EDF=∠EFD=60°,
∵DF∥BC,
∴∠BED=∠EDF=60°,∠CEF=∠DFE=60°,
∵AB⊥ED,AC⊥EF,
∴∠BDE=∠CFE=90°,
∴∠B=∠C=30°,
∴∠ADF=∠B=∠AFD=∠C=30°,
∴△ABC,△ADF是等腰三角形;
(2)∵△DEF的边长为3,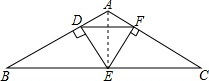
∴DE=EF=3,
在Rt△BDE与Rt△CEF中,
∵∠B=∠C=30°,
∴BE=CE=6,
连接AE,则AE⊥BC,
∴AB=AC=$\frac{\sqrt{3}}{2}$BE=3$\sqrt{3}$,
∴△ABC的周长=AB+AB+BC=6$\sqrt{3}$+6.
点评 本题考查了等腰三角形的判定和性质,等边三角形的性质,解直角三角形,熟练掌握等腰三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
7.若a2=7.856,b2=78.56,x2=785.6,下列关系正确的是( )
| A. | x=$\frac{a}{10}$ | B. | x=10b | C. | x=10a | D. | x=$\frac{b}{10}$ |
7.若点(-2,y1),(-1,y2),(1,y3)都在反比例函数y=-$\frac{2}{x}$的图象上,则( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y1>y3>y2 |