题目内容
4. 如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM,其中AM交直线DE于点N.若45°<∠CDE<90°,当MN=3,AN=4时,正方形ABCD的边长为( )
如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM,其中AM交直线DE于点N.若45°<∠CDE<90°,当MN=3,AN=4时,正方形ABCD的边长为( )| A. | $\sqrt{7}$ | B. | 5 | C. | 5$\sqrt{2}$ | D. | $\frac{5}{2}$$\sqrt{2}$ |
分析 连接CN、DM、AC,根据轴对称的性质可得CN=MN,CD=DM,∠DCN=∠DMN,根据正方形的四条边都相等可得AD=CD,然后求出AD=DM,根据等边对等角可得∠DAM=∠DMN,从而得到∠DCN=∠DAM,再求出∠ACN+∠CAN=90°,判断出△ACN是直角三角形,然后利用勾股定理列式求出AC,再根据正方形的边长等于对角线的$\frac{\sqrt{2}}{2}$倍求解.
解答 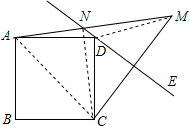 解:如图所示,连接CN、DM、AC,
解:如图所示,连接CN、DM、AC,
∵点C关于直线DE的对称点为M,
∴CN=MN,CD=DM,∠DCN=∠DMN,
在正方形ABCD中,AD=CD,
∴AD=DM,
∴∠DAM=∠DMN,
∴∠DCN=∠DAM,
∵∠ACN+∠CAN=∠BCD-∠DCN+∠CAD+∠DAM=∠BCD+∠CAD=90°,
∴∠ANC=180°-90°=90°,
∴△ACN是直角三角形,
由勾股定理得,AC=$\sqrt{A{N}^{2}+C{N}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴正方形ABCD的边长=$\frac{\sqrt{2}}{2}$AC=$\frac{\sqrt{2}}{2}$×5=$\frac{5}{2}$$\sqrt{2}$.
故选D.
点评 本题考查了正方形的性质,轴对称的性质,等边对等角的性质,勾股定理,作辅助线构造出等腰三角形与直角三角形是解题的关键,难点在于把AN、MN的长度以及正方形的对角线组成直角三角形.

练习册系列答案
相关题目
15.下列事件是不确定事件的是( )
| A. | 抛出的石块会下落 | |
| B. | 当室外温度低于-3℃时,将一碗清水放到室外,水会结冰 | |
| C. | 任意买一张电影票,座位号是奇数 | |
| D. | 地球绕着太阳转 |
16.-2016的相反数是( )
| A. | -2016 | B. | 2016 | C. | ±2016 | D. | $\frac{1}{2016}$ |
 如图,△ABC沿BC方向平移到△DEF的位置,若EF=5cm,CE=2cm,则AD的长为3cm.
如图,△ABC沿BC方向平移到△DEF的位置,若EF=5cm,CE=2cm,则AD的长为3cm. 如图是由几何相同的小正方体搭成的一个几何体,从左边看得到的平面图形是( )
如图是由几何相同的小正方体搭成的一个几何体,从左边看得到的平面图形是( )



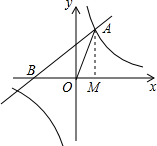 已知:如图,一次函数$y=\frac{{\sqrt{3}}}{3}x+m$与反比例函数$y=\frac{{\sqrt{3}}}{x}$的图象在第一象限的交点为A(1,n).
已知:如图,一次函数$y=\frac{{\sqrt{3}}}{3}x+m$与反比例函数$y=\frac{{\sqrt{3}}}{x}$的图象在第一象限的交点为A(1,n).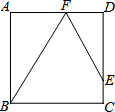 已知如图,正方形ABCD中,AD=4,点E在CD上,DE=3CE,F是AD上异于D的点,且∠EFB=∠FBC,则tan∠DFE=$\frac{15}{8}$.
已知如图,正方形ABCD中,AD=4,点E在CD上,DE=3CE,F是AD上异于D的点,且∠EFB=∠FBC,则tan∠DFE=$\frac{15}{8}$.