题目内容
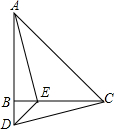 如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC上,且BE=BD,连结AE,DE,DC.
如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC上,且BE=BD,连结AE,DE,DC.(1)△ABE与△CBD全等吗?为什么?
(2)若∠BCD=15°,求∠CAE的度数.
考点:全等三角形的判定与性质
专题:
分析:(1)由已知条件根据SAS容易证明△ABE≌△CBD;
(2)先求出∠CAB=45°,再由△ABE≌△CBD得出∠BAE=∠BCD,即可求出∠CAE.
(2)先求出∠CAB=45°,再由△ABE≌△CBD得出∠BAE=∠BCD,即可求出∠CAE.
解答:
解:(1)△ABE≌△CBD;理由如下:
∵∠ABC=90°,
∴∠ABE=∠CBD=90°,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS);
(2)∵AB=CB,∠ABC=90°,
∴∠CAB=45°,
∵△ABE≌△CBD,
∴∠BAE=∠BCD=15°,
∴∠CAE=∠CAB-∠BAE=45°-15°=30°.
∵∠ABC=90°,
∴∠ABE=∠CBD=90°,
在△ABE和△CBD中,
|
∴△ABE≌△CBD(SAS);
(2)∵AB=CB,∠ABC=90°,
∴∠CAB=45°,
∵△ABE≌△CBD,
∴∠BAE=∠BCD=15°,
∴∠CAE=∠CAB-∠BAE=45°-15°=30°.
点评:本题考查了全等三角形的判定与性质;熟练掌握三角形全等的判定方法是解决问题的关键.

练习册系列答案
相关题目
下列说法中,正确的是( )
| A、一个数的倒数等于它本身的只有1 |
| B、一个数的平方根等于它本身的是1,0 |
| C、一个数的算术平方根等于它本身的只有1,0 |
| D、一个数的立方根等于它本身的只有1,0 |
 如图,AC平分∠BAD,∠B=∠D,AB=8cm,则AD=( )
如图,AC平分∠BAD,∠B=∠D,AB=8cm,则AD=( )| A、6cm | B、8cm |
| C、10cm | D、4cm |