题目内容
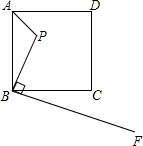 如图,已知点P是边长为4的正方形ABCD内的一点,且PB=3,BF⊥BP,请在射线BF找一点M,使点B,M,C为顶点的三角形与△ABP相似,求PM的长.
如图,已知点P是边长为4的正方形ABCD内的一点,且PB=3,BF⊥BP,请在射线BF找一点M,使点B,M,C为顶点的三角形与△ABP相似,求PM的长.考点:相似三角形的判定
专题:
分析:根据△ABP和△BMC相似可求得BM的长,再在Rt△PBM中利用勾股定理求PM即可.
解答:解:∵四边形ABCD为正方形,PB⊥BF,
∴∠ABC=∠PBF=90°,
∴∠ABP+∠PBC=∠PBC+∠CBF,
∴∠ABP=∠CBF,
当△ABP∽△CBM时,则有
=
,即
=
,解得BM=3,在Rt△PBM中,由勾股定理可求得PM=5;
当△ABP∽△MBC时,则有
=
,即
=
,解得BM=
,在Rt△PBM中,由勾股定理可求得PM=
;
综上可知PM为5或
.
∴∠ABC=∠PBF=90°,
∴∠ABP+∠PBC=∠PBC+∠CBF,
∴∠ABP=∠CBF,
当△ABP∽△CBM时,则有
| AB |
| BC |
| BP |
| BM |
| 4 |
| 4 |
| 3 |
| BM |
当△ABP∽△MBC时,则有
| AB |
| BM |
| BP |
| BC |
| 4 |
| BM |
| 3 |
| 4 |
| 16 |
| 3 |
| ||
| 3 |
综上可知PM为5或
| ||
| 3 |
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的对应边成比例是解题的关键,注意分类思想的应用.

练习册系列答案
相关题目
下列方程中是一元一次方程的是( )
| A、-5x+4=3y2 | ||||
| B、5(m2-1)=1-5m2 | ||||
C、2-
| ||||
| D、2(3p-2)=2p2 |
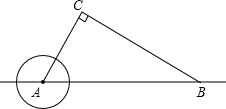 如图,△ABC中,∠C=90°,∠CBA=30°,BC=20
如图,△ABC中,∠C=90°,∠CBA=30°,BC=20