题目内容
已知抛物线y=a(x+4)2+4(a≠0)经过点(2,-2).
(1)求a的值;
(2)若点A(x1,y1),B(x2,y2)(x1<x2<-4)都在该抛物线上,试比较y1与y2的大小.
(1)求a的值;
(2)若点A(x1,y1),B(x2,y2)(x1<x2<-4)都在该抛物线上,试比较y1与y2的大小.
考点:二次函数图象上点的坐标特征
专题:
分析:(1)把点(2,-2)代入可求得a;
(2)由条件可知A、B两点都在对称轴左侧,利用二次函数的单调性质可比较大小
(2)由条件可知A、B两点都在对称轴左侧,利用二次函数的单调性质可比较大小
解答:解:
(1)∵抛物线过点(2,-2),
∴-2=a(2+4)2+4,解得a=-
;
(2)由(1)可知二次函数图象开口向下,在对称轴左侧,y随x的增大而增大,对称轴方程为x=-4,
∵x1<x2<-4,
∴A、B在对称左侧,
∴y1<y2.
(1)∵抛物线过点(2,-2),
∴-2=a(2+4)2+4,解得a=-
| 1 |
| 6 |
(2)由(1)可知二次函数图象开口向下,在对称轴左侧,y随x的增大而增大,对称轴方程为x=-4,
∵x1<x2<-4,
∴A、B在对称左侧,
∴y1<y2.
点评:本题主要考查待定系数法求解析式及二次函数的性质,掌握二次函数图象上点的坐标满足二次函数的解析式是解题的关键.

练习册系列答案
相关题目
在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,求旗杆的高度OM和玛丽在荡绳索过程中离地面的最低点的高度MN.


 墨墨在如图所示的△ABC的基础上作图,步骤如下:①分别以点A和点B为圆心,以a(a>
墨墨在如图所示的△ABC的基础上作图,步骤如下:①分别以点A和点B为圆心,以a(a>| 1 |
| 2 |
| 1 |
| 2 |
| A、AO=BO=CO |
| B、点O是△ABC的重心 |
| C、∠AOB=∠BOC |
| D、CO平分∠ACB |
 如图,△OAD≌△OBC,且∠O=70°,∠AEB=100°,则∠C=
如图,△OAD≌△OBC,且∠O=70°,∠AEB=100°,则∠C=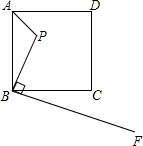 如图,已知点P是边长为4的正方形ABCD内的一点,且PB=3,BF⊥BP,请在射线BF找一点M,使点B,M,C为顶点的三角形与△ABP相似,求PM的长.
如图,已知点P是边长为4的正方形ABCD内的一点,且PB=3,BF⊥BP,请在射线BF找一点M,使点B,M,C为顶点的三角形与△ABP相似,求PM的长.