题目内容
1. 如图所示,一个寻宝探险队从A处出发探寻宝藏,他们向东行4km到达点C,然后又向正北方向走3km到达点D,接着他们又向正东方向行走2km到达点E,最后他们又向正北方向行走6km到达点B才找到了宝藏.若他们能直线行走,要少走多少路程?
如图所示,一个寻宝探险队从A处出发探寻宝藏,他们向东行4km到达点C,然后又向正北方向走3km到达点D,接着他们又向正东方向行走2km到达点E,最后他们又向正北方向行走6km到达点B才找到了宝藏.若他们能直线行走,要少走多少路程?
分析 延长BE、AC交于F,根据题意求出CF和AF的长,根据勾股定理计算出AB的长,根据题意计算即可.
解答 解: 延长BE、AC交于F,
延长BE、AC交于F,
由题意得,CF=DE=2km,则AF=AC+CF=6km,
EF=CD=3km,则BF=EF+BE=9km,
∴AB=$\sqrt{A{F}^{2}+B{F}^{2}}$=3$\sqrt{13}$km,
AF+BF-AB=(15-3$\sqrt{13}$)km,
答:直线行走,要少走(15-3$\sqrt{13}$)km路程.
点评 本题考查的是勾股定理的应用,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
相关题目
12.等腰三角形的周长为10,底边长y与腰x的函数关系式是y=10-2x,则自变量x的取值范围是( )
| A. | x>0 | B. | x<5 | C. | 0<x<5 | D. | 2.5<x<5 |
9.如果关于x的方程(m+1)x2+(m-1)x+m=0是一元一次方程,则m的值为( )
| A. | 1 | B. | -1 | C. | 0 | D. | 1或-1 |
6.下列方程中是一元一次方程的是( )
| A. | $\frac{2}{x}$+2=5 | B. | $\frac{3x-1}{2}$+4=3x | C. | y2+3y=0 | D. | 9x-y=2 |
13.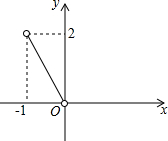 已知函数图象如图所示,则此函数解析式为( )
已知函数图象如图所示,则此函数解析式为( )
 已知函数图象如图所示,则此函数解析式为( )
已知函数图象如图所示,则此函数解析式为( )| A. | y=-2x | B. | y=-2x(-1<x<0) | C. | y=-$\frac{1}{2}$x | D. | y=-$\frac{1}{2}$x(-1<x<0) |
11.若a≠b,下列各式中不能成立的是( )
| A. | (a+b)2=(-a-b)2 | B. | (-a-b)(a-b)=(b+a)(b-a) | C. | (a-b)2n=(b-a)2n | D. | (a-b)3=(b-a)3 |