题目内容
2.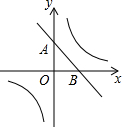 已知直线y=-x+b与双曲线y=$\frac{k}{x}$(k>0).
已知直线y=-x+b与双曲线y=$\frac{k}{x}$(k>0).(1)若b=1时,坐标原点关于直线AB的对称点正好落在双曲线上,求k的值;
(2)若k=1时,直线y=-x+b与双曲线有两个公共点,求b的取值范围.
分析 (1)根据题意求得对称点的坐标,然后根据反比例函数图象上点的坐标特征即可求得k的值;
(2)根据题意得到$\frac{1}{x}$=-x+b,整理得x2-bx+1=0,然后根据△>0,即可求得.
解答 解:(1)∵b=1时,直线为y=-x+b,
∴A(0,1),B(1,0),
∴原点关于直线AB的对称点为(1,1),
∴k=1×1=1;
(2)若k=1时,则双曲线y=$\frac{1}{x}$.
∵直线y=-x+b与双曲线有两个公共点,
∴$\frac{1}{x}$=-x+b,
整理得x2-bx+1=0,
∴b2-4>0,
∴b>2或b<-2.
点评 本题考查了一次函数和反比例函数的交点问题,用到的知识点为:若2个函数有两个交点,整理所得的一元二次方程的根的判别式大于0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限内作正方形ABCD,点D在双曲线y=$\frac{k}{x}$(k≠0)上,将正方形沿x轴负方向平移a个单位长度后,点C恰好落在该双曲线上,则a的值是2.
如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限内作正方形ABCD,点D在双曲线y=$\frac{k}{x}$(k≠0)上,将正方形沿x轴负方向平移a个单位长度后,点C恰好落在该双曲线上,则a的值是2.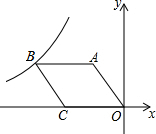 如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数y=$\frac{k}{x}$(x<0)的图象经过顶点B.
如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数y=$\frac{k}{x}$(x<0)的图象经过顶点B.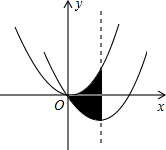 如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}$x2经过平移得到抛物线y=$\frac{1}{2}$x2-2x,求其对称轴与两段抛物线所围成的阴影部分的面积.
如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}$x2经过平移得到抛物线y=$\frac{1}{2}$x2-2x,求其对称轴与两段抛物线所围成的阴影部分的面积.