题目内容
4. 如图,B处在A处的南偏西40°方向,C处在A处的南偏东12°方向,C处在B处得北偏东80°方向,则∠ACB的度数为88度.
如图,B处在A处的南偏西40°方向,C处在A处的南偏东12°方向,C处在B处得北偏东80°方向,则∠ACB的度数为88度.
分析 根据方向角的定义,即可求得∠BAC,∠ABC的度数,然后根据三角形内角和定理即可求解.
解答 解:如图,
∵AE,DB是正南正北方向,
∴BD∥AE,
∵∠DBA=40°,
∴∠BAE=∠DBA=40°,
∵∠EAC=12°,
∴∠BAC=∠BAE+∠EAC=40°+12°=52°,
又∵∠DBC=80°,
∴∠ABC=80°-40°=40°,
∴∠ACB=180°-∠ABC-∠BAC=180°-52°-40°=88°,
故答案为:88.
点评 本题主要考查了方向角的定义,以及三角形的内角和定理,正确理解定义是解题的关键.

练习册系列答案
相关题目
14.若将代数式中的任意两个字母交换,代数式不变,则称这个代数式为完全对称式,如a+b+c就是完全对称式.下列三个代数式:
①(a-b)2;
②(2a-b)(2a+b);
③a(a+b).
其中是完全对称式的是( )
①(a-b)2;
②(2a-b)(2a+b);
③a(a+b).
其中是完全对称式的是( )
| A. | ③ | B. | ①③ | C. | ②③ | D. | ① |
15.下列实数是无理数的是( )
| A. | $\frac{\sqrt{4}}{3}$ | B. | 0 | C. | 0.$\stackrel{•}{7}$ | D. | $\root{3}{9}$ |
19. 如图,OD⊥AB于点O,若∠1=∠2,则图中互补的角共有( )
如图,OD⊥AB于点O,若∠1=∠2,则图中互补的角共有( )
 如图,OD⊥AB于点O,若∠1=∠2,则图中互补的角共有( )
如图,OD⊥AB于点O,若∠1=∠2,则图中互补的角共有( )| A. | 5对 | B. | 4对 | C. | 3对 | D. | 2对 |
 如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限内作正方形ABCD,点D在双曲线y=$\frac{k}{x}$(k≠0)上,将正方形沿x轴负方向平移a个单位长度后,点C恰好落在该双曲线上,则a的值是2.
如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限内作正方形ABCD,点D在双曲线y=$\frac{k}{x}$(k≠0)上,将正方形沿x轴负方向平移a个单位长度后,点C恰好落在该双曲线上,则a的值是2.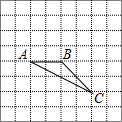 如图,在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上.
如图,在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上.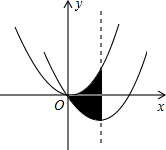 如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}$x2经过平移得到抛物线y=$\frac{1}{2}$x2-2x,求其对称轴与两段抛物线所围成的阴影部分的面积.
如图,在平面直角坐标系中,抛物线y=$\frac{1}{2}$x2经过平移得到抛物线y=$\frac{1}{2}$x2-2x,求其对称轴与两段抛物线所围成的阴影部分的面积.