题目内容
4.已知△ABC的三边为a,b,c且满足$\sqrt{a-b}$+|c2-a2-b2|=0,则△ABC是等腰直角三角形.分析 首先根据题意可得$\sqrt{a-b}$+|c2-a2-b2|=0,进而得到a2+b2=c2,a=b,根据勾股定理逆定理可得△ABC的形状为等腰直角三角形.
解答 解:$\sqrt{a-b}$+|c2-a2-b2|=0,
∴c2-a2-b2=0,a-b=0,
解得:a2+b2=c2,a=b,
∴△ABC的形状为等腰直角三角形.
故答案为:等腰直角.
点评 此题主要考查了勾股定理逆定理以及非负数的性质,关键是掌握勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
相关题目
14.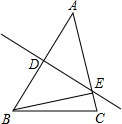 如图,在△ABC中,BC=4cm,AB的垂直平分线交AB于点D,交边AC点E,AC的长为6cm,则△BCE的周长等于( )
如图,在△ABC中,BC=4cm,AB的垂直平分线交AB于点D,交边AC点E,AC的长为6cm,则△BCE的周长等于( )
 如图,在△ABC中,BC=4cm,AB的垂直平分线交AB于点D,交边AC点E,AC的长为6cm,则△BCE的周长等于( )
如图,在△ABC中,BC=4cm,AB的垂直平分线交AB于点D,交边AC点E,AC的长为6cm,则△BCE的周长等于( )| A. | 8cm | B. | 10cm | C. | 12cm | D. | 13cm |
 如图.要判定AB∥CD,需要哪些条件?根据是什么?
如图.要判定AB∥CD,需要哪些条件?根据是什么?