题目内容
12.解方程:($\frac{x}{x-1}$)2+$\frac{5x}{x-1}$-6=0.分析 根据方程特点设y=$\frac{x}{x-1}$,则原方程可化为y2+5y-6=0.解一元二次方程求y,再求x.
解答 解:设$\frac{x}{x-1}$=y,则原方程化为y2+5y-6=0.
解得y1=-6,y2=1.
当y1=-6时,$\frac{x}{x-1}$=-6,解得x1=$\frac{6}{7}$,
当y2=1时,$\frac{x}{x-1}$=1.无解,
经检验x=$\frac{6}{7}$是原方程的根
∴原方程的根是x=$\frac{6}{7}$.
点评 用换元法解一些复杂的分式方程是比较简单的一种方法,根据方程特点设出相应未知数,解方程能够使问题简单化,注意求出方程解后要验根.

练习册系列答案
相关题目
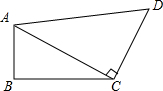 如图是一块四边形草坪ABCD,已知∠ACD=90°,AB=3m,BC=CD=4m,AD=$\sqrt{41}$m,求草坪的面积.
如图是一块四边形草坪ABCD,已知∠ACD=90°,AB=3m,BC=CD=4m,AD=$\sqrt{41}$m,求草坪的面积. 如图,AB>AC,AD⊥BC,AE平分∠BAC,求证:∠DAE=$\frac{1}{2}$(∠C-∠B).
如图,AB>AC,AD⊥BC,AE平分∠BAC,求证:∠DAE=$\frac{1}{2}$(∠C-∠B).