题目内容

已知：M=
a-ba+b+3
是a+b+3的算术平方根，N=
a-2b+2a+6b
是a+6b算术平方根，求M•N的值．
考点：算术平方根
专题：计算题
分析：根据题意列出关于a与b的方程组，求出方程组的解得到a与b的值，即可求出所求式子的值．
解答：解：根据题意得：
a-b=2
a-2b+2=2
，
解得：a=4，b=2，
∴M•N=
9
×
16
=3×4=12．
点评：此题考查了算术平方根，熟练掌握算术平方根的定义是解本题的关键．
练习册系列答案
相关题目
定义1：在△ABC中，若顶点A，B，C按逆时针方向排列，则规定它的面积为“有向面积”；若顶点A，B，C按顺时针方向排列，则规定它的面积的相反数为△ABC的“有向面积”．“有向面积”用
.
S
表示，例如图1中，
.
S △ABC
=S△ABC，图2中，
.
S △ABC
=-S△ABC．
定义2：在平面内任取一个△ABC和点P（点P不在△ABC的三边所在直线上），称有序数组（
.
S △PBC
，
.
S △PCA
，
.
S △PAB
）为点P关于△ABC的“面积坐标”，记作
.
P
(
.
S △PBC
，
.
S △PCA
，
.
S △PAB
)，例如图3中，菱形ABCD的边长为2，∠ABC=60°，则
.
S △ABC
=
3
，点D关于△ABC的“面积坐标”
.
D
(
.
S △DBC
，
.
S △DCA
，
.
S △DAB
)为
.
D
(
3
，-
3
，
3
)．
在图3中，我们知道S△ABC=S△DBC+S△DAB-S△DCA，利用“有向面积”，我们也可以把上式表示为：
.
S △ABC
=
.
S △DBC
+
.
S △DAB
+
.
S △DCA
．
应用新知：
（1）如图4，正方形ABCD的边长为1，则
.
S △ABC
=
 
，点D关于△ABC的“面积坐标”是
 
；
探究发现：
（2）在平面直角坐标系xOy中，点A（0，2），B（-1，0）．
①若点P是第二象限内任意一点（不在直线AB上），设点P关于△ABO的“面积坐标”为
.
P
（m，n，k），试探究m+n+k与
.
S △ABO
之间有怎样的数量关系，并说明理由；
②若点P（x，y）是第四象限内任意一点，请直接写出点P关于△ABO的“面积坐标”（用x，y表示）；
解决问题：
（3）在（2）的条件下，点C（1，0），D（0，1），点Q在抛物线y=x2+2x+4上，求当S△QAB+S△QCD的值最小时，点Q的横坐标．
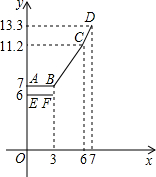为缓解油价上涨给出租车行业带来的成本压力，某市自2007年11月17日起，调整出租车运价，调整方案见下列表格及图象（其中a，b，c为常数）
行驶路程 收费标准
调价前 调价后
不超过3km的部分 起步价6元 起步价a元
超过3km不超出6km的部分 每公里2.1元 每公里b元
超出6km的部分 每公里c元
设行驶路程xkm时，调价前的运价y1（元），调价后的运价为y2（元），如图，折线ABCD表示y2与x之间的关系式，线段EF表示当0≤x≤3时，y1与x的函数关系式，根据图表信息，完成下列各题：
①填空：a=
 
，b=
 
，c=
 
；
②写出当x＞3时，y1与x的关系式；
③设行驶路程10km时，对于乘客来说调价前的运价y1（元），调价后的运价为y2（元）哪个更合算，为什么？
化简（a3-2b3）+2（ab2-
1
2
a2b）-2（ab2-b3）．
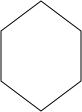如图，表示一个正六菱柱形状的高大建筑物的俯视图．若该建筑物的高度为150米，底面正六边形的边长为50米．
（1）画出它的主视图；
（2）求该建筑物的体积．
解方程组：
2x-1=5y
3x-5y=5
．
若最简二次根式
3b-1a+2
与
4b-a
是同类二次根式，则a=
 
，b=
 
．
四张卡片分别标有0、1、2、3的数字，抽出一张的数字是偶数的概率是
 
．
如果甲在乙北偏东40°的方向上，那么乙在甲
 
的方向上．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网