题目内容
8. 如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO.有下列结论:
如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO.有下列结论:①AC⊥BD;
②AC平分∠BCD;
③△BCD是等腰三角形;
④∠BAD=90°
其中正确结论的序号是①②③(把所有正确结论的序号都填在横线上)
分析 ①根据全等三角形的性质可得出∠AOB=∠AOD=90°,进而可得出AC⊥BD,结论①正确;②根据全等三角形的性质可得出BO=OD,由垂直可得出∠BOC=∠DOC=90°,结合公共边OC=OC可证出△BOD≌△DOC(SAS),根据全等三角形的性质可得出BC=DC,∠BCO=∠DCO,由此可得出AC平分∠BCD,结论②正确;由BC=DC可得出△BCD是等腰三角形,结论③正确;④根据全等三角形的性质无法得出∠BAD的度数,即结论④错误.综上即可得出结论.
解答 解:①∵△ABO≌△ADO,
∴∠AOB=∠AOD=$\frac{1}{2}$×180°=90°,
∴AC⊥BD,结论①正确;
②∵△ABO≌△ADO,
∴BO=OD.
∵AC⊥BD,
∴∠BOC=∠DOC=90°.
在△BOD和△DOC中,$\left\{\begin{array}{l}{BO=DO}\\{∠BOC=∠DOC}\\{OC=OC}\end{array}\right.$,
∴△BOD≌△DOC(SAS),
∴BC=DC,∠BCO=∠DCO,
∴AC平分∠BCD,结论②正确;
③∵BC=DC,
∴△BCD是等腰三角形,结论③正确;
④∵无法求出∠BAD的度数,
∴∠BAD未知,结论④错误.
故答案为:①②③.
点评 本题考查了全等三角形的判定与性质、等腰三角形的判定与性质以及垂直,根据全等三角形的判定与性质逐一分析四条结论的正误是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.355、444、533的大小关系是( )
| A. | 355<444<533 | B. | 444<355<533 | C. | 533<444<355 | D. | 533<355<444 |
3.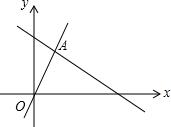 如图,函数y=2x和y=ax+1的图象相交于A(m,3),则不等式2x<ax+1的解集为( )
如图,函数y=2x和y=ax+1的图象相交于A(m,3),则不等式2x<ax+1的解集为( )
 如图,函数y=2x和y=ax+1的图象相交于A(m,3),则不等式2x<ax+1的解集为( )
如图,函数y=2x和y=ax+1的图象相交于A(m,3),则不等式2x<ax+1的解集为( )| A. | x<$\frac{3}{2}$ | B. | x<3 | C. | x>$\frac{3}{2}$ | D. | x>3 |
13.不等式2x<4的解集为( )
| A. | x<$\frac{1}{2}$ | B. | x<2 | C. | x>$\frac{1}{2}$ | D. | x>2 |
20. 如图,四边形ABCD是平行四边形,则下列结论:①若AB=BC,则四边形ABCD一定是菱形;②若AC⊥BD,则四边形ABCD一定是矩形;③若∠ABC=90°,则四边形ABCD一定是菱形;④若AC=BD,则四边形ABCD一定是正方形.其中正确的有( )
如图,四边形ABCD是平行四边形,则下列结论:①若AB=BC,则四边形ABCD一定是菱形;②若AC⊥BD,则四边形ABCD一定是矩形;③若∠ABC=90°,则四边形ABCD一定是菱形;④若AC=BD,则四边形ABCD一定是正方形.其中正确的有( )
 如图,四边形ABCD是平行四边形,则下列结论:①若AB=BC,则四边形ABCD一定是菱形;②若AC⊥BD,则四边形ABCD一定是矩形;③若∠ABC=90°,则四边形ABCD一定是菱形;④若AC=BD,则四边形ABCD一定是正方形.其中正确的有( )
如图,四边形ABCD是平行四边形,则下列结论:①若AB=BC,则四边形ABCD一定是菱形;②若AC⊥BD,则四边形ABCD一定是矩形;③若∠ABC=90°,则四边形ABCD一定是菱形;④若AC=BD,则四边形ABCD一定是正方形.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.某种服装的进价为240元,出售时标价为330元,由于换季,商店准备打折销售,但要保持利润不低于10%,那么至多打( )
| A. | 6折 | B. | 7折 | C. | 8折 | D. | 9折 |
18. 如图,在?ABCD中,AD=8,AB=6,DE平分∠ADC交BC于点E,则BE的长是( )
如图,在?ABCD中,AD=8,AB=6,DE平分∠ADC交BC于点E,则BE的长是( )
 如图,在?ABCD中,AD=8,AB=6,DE平分∠ADC交BC于点E,则BE的长是( )
如图,在?ABCD中,AD=8,AB=6,DE平分∠ADC交BC于点E,则BE的长是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 如图所示,在?ABCD中,对角线AC,BC相交于点O,已知△BOC与△AOB的周长之差为4,?ABCD的周长为28,则BC的长度为( )
如图所示,在?ABCD中,对角线AC,BC相交于点O,已知△BOC与△AOB的周长之差为4,?ABCD的周长为28,则BC的长度为( ) 若将三个数$\sqrt{3}$,3$\sqrt{2}$,2$\sqrt{3}$表示在数轴上,则能被如图所示的墨迹覆盖的数是$\sqrt{3}$.
若将三个数$\sqrt{3}$,3$\sqrt{2}$,2$\sqrt{3}$表示在数轴上,则能被如图所示的墨迹覆盖的数是$\sqrt{3}$.