题目内容
19. 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明:DC=BE.
分析 (1)根据等腰直角三角形的性质可以得出△ABE≌△ACD;
(2)由△ABE≌△ACD,即可得出结论.
解答 (1)解:△ABE≌△ACD;理由如下:
∵△ABC和△ADE是等腰直角三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=90°,
∴∠BAC+∠EAC=∠DAE+∠EAC,
∴∠BAE=∠CAD,
在△ABE和△ACD中,$\left\{\begin{array}{l}{AB=AC}&{\;}\\{∠BAE=∠CAD}&{\;}\\{AE=AD}&{\;}\end{array}\right.$,
∴△ABE≌△ACD(SAS)
(2)证明:由(1)得:△ABE≌△ACD,
∴DC=BE.
点评 本题考查了等腰直角三角形的性质的运用,全等三角形的判定及性质的运用,垂直的判定的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
10. 如图所示的两个三角形相似,则α与β的度数分别为( )
如图所示的两个三角形相似,则α与β的度数分别为( )
 如图所示的两个三角形相似,则α与β的度数分别为( )
如图所示的两个三角形相似,则α与β的度数分别为( )| A. | α=30°,β=30° | B. | α=105°,β=30° | C. | α=30°,β=105° | D. | α=105°,β=45° |
7.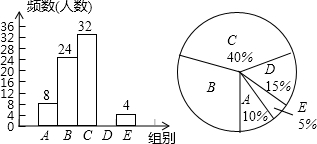 网络技术的发展对学生学习方式产生巨大的影响,某校为了解学生每周课余利用网络资源进行自主学习的时间,在本校随机抽取若干名学生进行问卷调查,下面是根据调查结果绘制成的不完整的统计图表:
网络技术的发展对学生学习方式产生巨大的影响,某校为了解学生每周课余利用网络资源进行自主学习的时间,在本校随机抽取若干名学生进行问卷调查,下面是根据调查结果绘制成的不完整的统计图表:
请根据图表中的信息解答下列问题:
(1)表中的n=12,扇形统计图中B组对应的圆心角为108°;
(2)请补全频数分布直方图;
(3)该校准备召开利用网络资源进行自主学习的交流会,计划在E组学生中随机选出两人进行经验介绍,已知E组的四名学生中,七、八年级各有1人,九年级有2人,请用画树状图法或列表法求抽取的两名学生都来自九年级的概率.
 网络技术的发展对学生学习方式产生巨大的影响,某校为了解学生每周课余利用网络资源进行自主学习的时间,在本校随机抽取若干名学生进行问卷调查,下面是根据调查结果绘制成的不完整的统计图表:
网络技术的发展对学生学习方式产生巨大的影响,某校为了解学生每周课余利用网络资源进行自主学习的时间,在本校随机抽取若干名学生进行问卷调查,下面是根据调查结果绘制成的不完整的统计图表:请根据图表中的信息解答下列问题:
| 组别 | 学习时间x(h) | 频数(人数) |
| A | 0<x≤1 | 8 |
| B | 1<x≤2 | 24 |
| C | 2<x≤3 | 32 |
| D | 3<x≤4 | n |
| E | 4小时以上 | 4 |
(2)请补全频数分布直方图;
(3)该校准备召开利用网络资源进行自主学习的交流会,计划在E组学生中随机选出两人进行经验介绍,已知E组的四名学生中,七、八年级各有1人,九年级有2人,请用画树状图法或列表法求抽取的两名学生都来自九年级的概率.
11.下列各式中属于最简分式的是( )
| A. | $\frac{{2{x^2}}}{x}$ | B. | a+b | C. | $\frac{1}{2x+1}$ | D. | $\frac{2x-2}{x-1}$ |
9.下列说法正确的是( )
| A. | 40°50′=40.5° | |
| B. | 若线段AP=BP,则P一定是AB中点 | |
| C. | 若∠AOC=$\frac{1}{2}$∠AOB,则OC是∠AOB的平分线 | |
| D. | 连结两点的线段的长度叫做两点之间的距离 |
 已知:如图,在正方形ABCD中,F是AB上一点,延长CB到E,使BE=BF,连接CF并延长交AE于G.
已知:如图,在正方形ABCD中,F是AB上一点,延长CB到E,使BE=BF,连接CF并延长交AE于G.