题目内容
8. 如图是一个正方体的展开图,标注了字母“a”的面是正方体的正面,已知正方体相对两个面上的代数式的值相等.求a+$\sqrt{x+y}$的值.
如图是一个正方体的展开图,标注了字母“a”的面是正方体的正面,已知正方体相对两个面上的代数式的值相等.求a+$\sqrt{x+y}$的值.
分析 正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答列方程组求出x、y的值,再确定出a的值,然后代入代数式进行计算即可得解.
解答 解:由题意得,$\left\{\begin{array}{l}{y=2x-5①}\\{5-x=y+1②}\end{array}\right.$,
①代入②得,5-x=2x-5+1,
解得x=3,
将x=3代入①得,y=2×3-5=1,
所以,$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$,
又∵正方体相对两个面上的代数式的值相等,
∴a=3,
所以,a+$\sqrt{x+y}$=3+$\sqrt{3+1}$=3+2=5.
点评 本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5. 如图,在x轴上有两点A(-3,0)和B(3,0),有一动点C在线段AB上从点A运动到点B(不与A,B重合),分别以AC,BC为底边作等腰△AEC和等腰△BFC,顶点E,F恰好落在反比例函数y=-$\frac{5}{x}$(x<0)和y=$\frac{2}{x}$(x>0)的图象上,连结EF,在整个运动过程中,线段EF长度的变化情况是( )
如图,在x轴上有两点A(-3,0)和B(3,0),有一动点C在线段AB上从点A运动到点B(不与A,B重合),分别以AC,BC为底边作等腰△AEC和等腰△BFC,顶点E,F恰好落在反比例函数y=-$\frac{5}{x}$(x<0)和y=$\frac{2}{x}$(x>0)的图象上,连结EF,在整个运动过程中,线段EF长度的变化情况是( )
 如图,在x轴上有两点A(-3,0)和B(3,0),有一动点C在线段AB上从点A运动到点B(不与A,B重合),分别以AC,BC为底边作等腰△AEC和等腰△BFC,顶点E,F恰好落在反比例函数y=-$\frac{5}{x}$(x<0)和y=$\frac{2}{x}$(x>0)的图象上,连结EF,在整个运动过程中,线段EF长度的变化情况是( )
如图,在x轴上有两点A(-3,0)和B(3,0),有一动点C在线段AB上从点A运动到点B(不与A,B重合),分别以AC,BC为底边作等腰△AEC和等腰△BFC,顶点E,F恰好落在反比例函数y=-$\frac{5}{x}$(x<0)和y=$\frac{2}{x}$(x>0)的图象上,连结EF,在整个运动过程中,线段EF长度的变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先增大后减小 | D. | 先减小后增大 |
16.为了让同学们了解自己的体育水平,初二1班的体育康老师对全班45名学生进行了一次体育模拟测试(得分均为整数)成绩满分为10分,成绩达到9分以上(包含9分)为优秀,成绩达到6分以上(包含6分)为合格,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下:

初二1班体育模拟测试成绩分析表
根据以上信息,解答下列问题:
(1)在这次测试中,该班女生得10分的人数为4人,则这个班共有女生25人;
(2)补全初二1班男生体育模拟测试成绩统计图,并把相应的数据标注在统计图上;
(3)补全初二1班体育模拟测试成绩分析表;
(4)你认为在这次体育测试中,1班的男生队、女生队哪个表现更突出一些?并写出一条支持你的看法的理由;
(5)体育康老师说,从整体看,1班的体育成绩在合格率方面基本达标,但在优秀率方面还不够理想,因此他希望全班同学继续加强体育锻炼,争取在期末考试中,全班的优秀率达到60%,若男生优秀人数再增加6人,则女生优秀人数再增加多少人才能完成康老师提出的目标?

初二1班体育模拟测试成绩分析表
| 平均分 | 方差 | 中位数 | 众数 | 合格率 | 优秀率 | |
| 男生 | 2 | 8 | 7 | 95% | 40% | |
| 女生 | 7.92 | 1.99 | 8 | 96% | 36% |
(1)在这次测试中,该班女生得10分的人数为4人,则这个班共有女生25人;
(2)补全初二1班男生体育模拟测试成绩统计图,并把相应的数据标注在统计图上;
(3)补全初二1班体育模拟测试成绩分析表;
(4)你认为在这次体育测试中,1班的男生队、女生队哪个表现更突出一些?并写出一条支持你的看法的理由;
(5)体育康老师说,从整体看,1班的体育成绩在合格率方面基本达标,但在优秀率方面还不够理想,因此他希望全班同学继续加强体育锻炼,争取在期末考试中,全班的优秀率达到60%,若男生优秀人数再增加6人,则女生优秀人数再增加多少人才能完成康老师提出的目标?
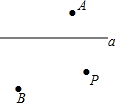 如图,平面上有直线a及直线a外的三点A、B、P.
如图,平面上有直线a及直线a外的三点A、B、P.
 对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数;用max{a,b,c}表示这三个数中最大的数.
对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数;用max{a,b,c}表示这三个数中最大的数. 在20km的越野比赛中,甲乙两选手均跑完全程,他们的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,解答下列问题:
在20km的越野比赛中,甲乙两选手均跑完全程,他们的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,解答下列问题: