题目内容
 一辆汽车和一辆摩托车分别从A,B两地去C地,它们离A地的路程随时间变化的图象如图所示.则当汽车到达C地时,摩托车距离C地的路程为( )
一辆汽车和一辆摩托车分别从A,B两地去C地,它们离A地的路程随时间变化的图象如图所示.则当汽车到达C地时,摩托车距离C地的路程为( )| A、140km | B、40km |
| C、60km | D、45km |
考点:一次函数的应用
专题:
分析:设摩托车走的路程y与时间x之间的函数关系式为y=kx+b,由待定系数法求出函数关系式,当x=3时,求出就可以求出摩托车行驶的距离,就可以得出结论.
解答:解:设摩托车走的路程y与时间x之间的函数关系式为y=kx+b,由题意,得
,
解得:
,
则y=40x+20.
当x=3时,
y=40×3+20=140.
摩托车距离C地的路程为:180-140=40km.
故选B.
|
解得:
|
则y=40x+20.
当x=3时,
y=40×3+20=140.
摩托车距离C地的路程为:180-140=40km.
故选B.
点评:本题考查了行程问题的数量关系的运用,待定系数法求一次函数的解析式的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
下列水平放置的几何体中,主视图是矩形的有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
把二次函数y=x2+2x-1的图象向右平移2个单位,再向上平移3个单位,所得到图象的函数解析式是( )
| A、y=(x+1)2+1 |
| B、y=(x+1)2-1 |
| C、y=(x-1)2+1 |
| D、y=(x-1)2-1 |
下列各组数中互为相反数的是( )
A、3和
| |||
B、-
| |||
C、-3和
| |||
| D、-|-3|和-(-3) |
若方程(a2-1)x2+(a-1)x+(2a+1)y=0是二元一次方程,则a的值为( )
| A、1 | B、-1 | C、±1 | D、一切实数 |
若正比例函数y=kx经过点(1,2),则反比例函数y=
,下列说法不正确的是( )
| k |
| x |
| A、点(-2,-1)在它的图象上 |
| B、它的图象在第一、三象限 |
| C、当x>0时,y随x的增大而增大 |
| D、当x<0时,y随x的增大而减小 |
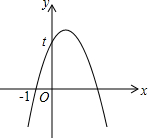 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,t).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,t).