题目内容
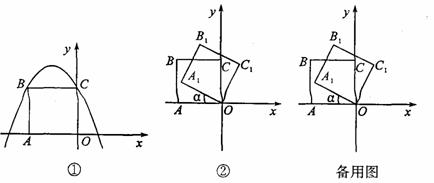
如图①,在平面直角坐标系中,二次函数y=-x2-2x+2的图像与y轴交于点C,以OC为一边向左侧作正方形OCBA.
(1)判断点B是否在二次函数y=-x2-2x+2的图像上,并说明理由;
(2)用配方法求二次函数y=-x2-2x+2的图像的对称轴;
(3)如图②,把正方形OCBA绕点O顺时针旋转a后得到正方形A1B1C1O(0°<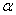 <90°).
<90°).
①当tan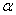 =
=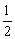 时,二次函数y=-x2-2x+2的图像的对称轴上是否存在一点P,使△PB1C1为直角三角形?若存在,请求出所有点P的坐标;若不存在,请说明理由,
时,二次函数y=-x2-2x+2的图像的对称轴上是否存在一点P,使△PB1C1为直角三角形?若存在,请求出所有点P的坐标;若不存在,请说明理由,
②在二次函数y=-x2-2x+2的图像的对称轴上是否存在一点P,使△PB1C1为等腰直角三角形?若存在,请直接写出此时tan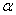 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1) (2)x=-1.(3)①存在.P1 (-1, 2 -2) , P2(-1,-2) , P3(-1,
-2) , P2(-1,-2) , P3(-1, ) .②存在.tan
) .②存在.tan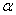 =
=

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
二次函数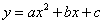 (a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
| X | ﹣1 | 0 | 1 | 3 |
| y | ﹣1 | 3 | 5 | 3 |
下列结论:
(1)ac<0;(2)当x>1时,y的值随x值的增大而减小.
(3)3是方程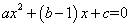 的一个根;
的一个根;
(4)当﹣1<x<3时,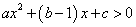 .
.
其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
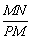 =1.
=1. (x>0)和y=
(x>0)和y=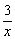 (x>0)于点P、M、N时,有=
(x>0)于点P、M、N时,有=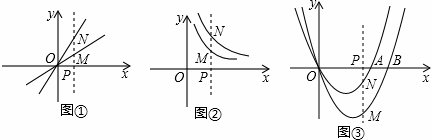
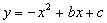 与x轴交与A(1,0),B(- 3,0)两点,
与x轴交与A(1,0),B(- 3,0)两点, 该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
