题目内容
19.把下列各式分解因式:(1)-4kx-8ky=-4k(x+2y)
(2)-8m2n-2mn=-2mn(4m+1)
(3)4(x-y)3-8x(y-x)2=-4(x-y)2(x+y).
分析 (1)原式提取公因式即可得到结果;
(2)原式提取公因式即可得到结果;
(3)原式变形后,提取公因式即可得到结果.
解答 解:(1)原式=-4k(x+2y);
(2)原式=-2mn(4m+1);
(3)原式=4(x-y)2[(x-y)-2x]=-4(x-y)2(x+y).
故答案为:(1)-4k(x+2y);(2)-2mn(4m+1);(3)-4(x-y)2(x+y).
点评 此题考查了因式分解-提公因式法,熟练掌握提取公因式的方法是解本题的关键.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
9.-5的倒数是( )
| A. | 5 | B. | $\frac{1}{5}$ | C. | -$\frac{1}{5}$ | D. | 25 |
13.运算结果为4x2-4xy+y2的是( )
| A. | (x-2y)2 | B. | (4x-y)2 | C. | (-2x-y)2 | D. | (2x-y)2 |
 如图,AB∥CD,AD∥BC,OE=OF,图中全等三角形共有6对.
如图,AB∥CD,AD∥BC,OE=OF,图中全等三角形共有6对.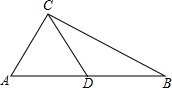 如图,在Rt△ABC中,CD是斜边AB的中线,AC=9cm,BC=40cm,求:
如图,在Rt△ABC中,CD是斜边AB的中线,AC=9cm,BC=40cm,求: 已知:如图,在四边形ABCD中,A′B′∥AB,A′D′∥AD,求证:△ABD∽△A′B′D′.
已知:如图,在四边形ABCD中,A′B′∥AB,A′D′∥AD,求证:△ABD∽△A′B′D′.