题目内容
9. 如图所示,已知△ABC与△A′B′C′,AD⊥BC于D,A′D′⊥B′C′于D′,且$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,∠B=∠B′,试说明△ABC∽△A′B′C′.
如图所示,已知△ABC与△A′B′C′,AD⊥BC于D,A′D′⊥B′C′于D′,且$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,∠B=∠B′,试说明△ABC∽△A′B′C′.
分析 先证明△ABD∽△A′B′D′,得出∠BAD=∠B′A′D′,$\frac{AD}{A′D′}=\frac{AB}{A′B′}$,证出$\frac{AD}{A′D′}=\frac{AC}{A′C′}$,再证明Rt△ADC∽Rt△A′D′C′,得出对应角相等∠DAC=∠D′A′C′,得出∠BAC=∠B′A′C′,即可得出结论.
解答 证明:∵AD⊥BC于D,A′D′⊥B′C′于D′,
∴∠ADB=∠ADC=∠A′D′B′=∠A′D′C′=90°,
∵∠B=∠B′,
∴△ABD∽△A′B′D′,
∴∠BAD=∠B′A′D′,$\frac{AD}{A′D′}=\frac{AB}{A′B′}$,
∵$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,
∴$\frac{AD}{A′D′}=\frac{AC}{A′C′}$,
∴Rt△ADC∽Rt△A′D′C′,
∴∠DAC=∠D′A′C′,
∴∠BAC=∠B′A′C′,
又∵$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,
∴△ABC∽△A′B′C′.
点评 本题考查了相似三角形的判定与性质;熟练掌握相似三角形的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列各数:-5,2,-3,1,$\frac{1}{2}$中,正整数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.计算(1-22)×3的结果是( )
| A. | -9 | B. | -11 | C. | 3 | D. | 6 |
4.为了了解学校开展“尊敬父母,从家务事做起”活动的实施情况,该校抽取初二年级50名学生,调查他们一周(按七天计算)的家务所用时间(单位:小时),得到一组数据,并绘制成下表,请根据该表完成下列各题:
(1)填写频率分布表中未完成的部分;
(2)这组数据的中位数落在什么范围内;
(3)由以上信息判断,每周做家务的时间不超过1.5小时的学生所占的百分比.
频数分布表
(1)填写频率分布表中未完成的部分;
(2)这组数据的中位数落在什么范围内;
(3)由以上信息判断,每周做家务的时间不超过1.5小时的学生所占的百分比.
频数分布表
| 分组 | 频数累计 | 频数 | 频率 |
| 0.55~1.05 | 正正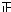 | 14 | 0.28 |
| 1.05~1.55 | 正正正 | 15 | 0.30 |
| 1.55~2.05 | 正 | 7 | 0.14 |
| 2.05~2.55 | 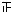 | 4 | 0.08 |
| 2.55~3.05 | 正 | 5 | 0.10 |
| 3.05~3.55 | 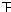 | 3 | 0.06 |
| 3.55~4.05 | 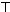 | 2 | 0.04 |
| 合计 | 50 | 1.00 |
 已知:如图,在四边形ABCD中,A′B′∥AB,A′D′∥AD,求证:△ABD∽△A′B′D′.
已知:如图,在四边形ABCD中,A′B′∥AB,A′D′∥AD,求证:△ABD∽△A′B′D′.