题目内容
18.某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现;当销售单价25元/件时,每天的销售量是250件,销售单价每上涨1元,每天的销售量就减少10件.(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大?最大利润是多少?
分析 (1)利用每件利润×销量=总利润,进而得出w与x的函数关系式;
(2)利用配方法求出二次函数最值进而得出答案.
解答 解:(1)由题意可得:w=(x-20)[250-10(x-25)]
=-10(x-20)(x-50)
=-10x2+700x-10000;
(2)∵w=-10x2+700x-10000=-10(x-35)2+2250,
∴当x=35时,w取到最大值2250,
即销售单价为35元时,每天销售利润最大,最大利润为2250元.
点评 此题主要考查了二次函数的应用,根据销量与售价之间的关系得出函数关系式是解题关键.

练习册系列答案
相关题目
9. 如图,与∠1是同旁内角的是( )
如图,与∠1是同旁内角的是( )
 如图,与∠1是同旁内角的是( )
如图,与∠1是同旁内角的是( )| A. | ∠2 | B. | ∠3 | C. | ∠4 | D. | ∠5 |
3.某校150名学生参加数学竞赛,平均分为75分,其中及格学生平均得85分,不及格学生平均得55分,则不及格学生人数为( )
| A. | 40 | B. | 48 | C. | 50 | D. | 100 |
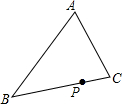 如图,点P在△ABC是边上一定点,请你找到一条过点P的直线,把△ABC分成面积相等的两部分,在图中画出这条直线并叙述画法:取AB中点D,过点D作DE∥AP交AB于点E,交AD与点H,连接EP,即为所求..
如图,点P在△ABC是边上一定点,请你找到一条过点P的直线,把△ABC分成面积相等的两部分,在图中画出这条直线并叙述画法:取AB中点D,过点D作DE∥AP交AB于点E,交AD与点H,连接EP,即为所求..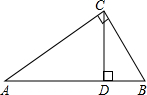 如图所示,在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D,AB=4cm,求BC,AD,BD的长及∠BCD的度数.
如图所示,在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D,AB=4cm,求BC,AD,BD的长及∠BCD的度数.