题目内容
19.(1)x≠1时,分式$\frac{2x}{x-1}$有意义.(2)x=0时,分式$\frac{2x}{x-1}$值为零.
(3)x>1或x<0时,分式$\frac{2x}{x-1}$值为正数
(4)整数x=0,2,3,-1时,分式$\frac{2x}{x-1}$值为整数.
分析 (1)根据分式有意义的条件得到x-1≠0,然后解不等式即可;
(2)根据分式的值为0可得:2x=0,x-1≠0据此可以解答本题;
(3)由于分式$\frac{2x}{x-1}$的值为正数,则分式的分子与分母同号,得到$\left\{\begin{array}{l}{2x>0}\\{x-1>0}\end{array}\right.$或$\left\{\begin{array}{l}{2x<0}\\{x-1<0}\end{array}\right.$,然后解两个不等式组即可;
(4)首先化简分式可得2$+\frac{2}{x-1}$,要使它的值为整数,则x-1应是2的约数,即x-1=±1,±2,进而解出x的值.
解答 解:(1)根据题意得x-1≠0,解得x≠1,
所以x≠1时分式有意义,
故答案为:≠1;
(2)由题意可得:x-1≠0且2x=0,
解得x=0,
故答案为:=0;
(3)∵分式$\frac{2x}{x-1}$值为正数,
∴$\left\{\begin{array}{l}{2x>0}\\{x-1>0}\end{array}\right.$或$\left\{\begin{array}{l}{2x<0}\\{x-1<0}\end{array}\right.$,
解得:x>1或x<0,
故答案为:>1或x<0;
(4)∵$\frac{2x}{x-1}$=2$+\frac{2}{x-1}$,
∴根据题意,得x-1=±1,±2,
解得x=0,2,3,-1,
又∵x取整数,
∴x的整数值为0,2,3,-1,
故答案为:=0,2,3,-1.
点评 本题主要考查了分式的值,(1)分式有意义的条件是分母不等于零.(2)分式无意义的条件是分母等于零.(3)分式的值为正数的条件是分子、分母同号.(4)分式的值为负数的条件是分子、分母异号,将分式适当的变形、转化是解答此题的关键.

 一个广告公司制作广告的收费标准是:以面积为单位,在不超过规定面积a(m2)的范围内,每张广告收费100元,若超过am2,则除了要交这100元的基本广告费以外,超过部分还要按每平方米5a元缴费.如表是该公司对两家用户广告的面积及相应收费情况的记载:
一个广告公司制作广告的收费标准是:以面积为单位,在不超过规定面积a(m2)的范围内,每张广告收费100元,若超过am2,则除了要交这100元的基本广告费以外,超过部分还要按每平方米5a元缴费.如表是该公司对两家用户广告的面积及相应收费情况的记载:| 单位 | 广告的面积(m2) | 收费金额(元) |
| 烟草公司 | 6 | 140 |
| 食品公司 | 3 | 100 |
(1)求a的值;
(2)求矩形ABCD的长和宽各是多少?(参考数据:1152=13225,232=529)
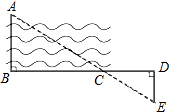 如图所示,要测量河两岸相对的两点A,B的距离,先从B处出发与AB成90°角方向,向前走80米到C处立一标杆,然后方向不变向前走50米至D处,在D处转90°,沿DE方向走30米,到E处,使A(目标物),C(标杆)与E在同一条直线上,那么可测得A,B间的距离是多少?
如图所示,要测量河两岸相对的两点A,B的距离,先从B处出发与AB成90°角方向,向前走80米到C处立一标杆,然后方向不变向前走50米至D处,在D处转90°,沿DE方向走30米,到E处,使A(目标物),C(标杆)与E在同一条直线上,那么可测得A,B间的距离是多少? 如图,在△ABC中,∠C=90°,∠B=30°,D为AB上一点,DE⊥BC于E.若BE=AC,DE+BC=3,求BD的长.
如图,在△ABC中,∠C=90°,∠B=30°,D为AB上一点,DE⊥BC于E.若BE=AC,DE+BC=3,求BD的长. 如图,矩形ABCD中,点B的坐标是(4,3),直线l平行于对角线AC,直线l从原点出发,沿x轴的正方向以每秒1个单位长度运动,与矩形OABC的两边分别交于点M,N,当MN=$\frac{1}{2}$AC时,直线l运动的时间是( )
如图,矩形ABCD中,点B的坐标是(4,3),直线l平行于对角线AC,直线l从原点出发,沿x轴的正方向以每秒1个单位长度运动,与矩形OABC的两边分别交于点M,N,当MN=$\frac{1}{2}$AC时,直线l运动的时间是( ) 如图,Rt△ABC中,∠ACB=90°,AC=BC,D为AC边上一动点,以BD为边向上作正方形BDEF,O是正方形的对称中心,直线CO分别交BD,EF于点M,N,求证:
如图,Rt△ABC中,∠ACB=90°,AC=BC,D为AC边上一动点,以BD为边向上作正方形BDEF,O是正方形的对称中心,直线CO分别交BD,EF于点M,N,求证: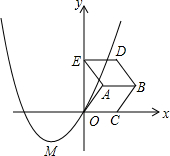 如图,在平面直角坐标系中,过原点的抛物线的顶点M的坐标为(-1,-1),点A的坐标为(1,1),以OA为边的菱形OABC的顶点C在x轴的正半轴上,把菱形OABC沿AB向上翻折得到菱形ABDE.
如图,在平面直角坐标系中,过原点的抛物线的顶点M的坐标为(-1,-1),点A的坐标为(1,1),以OA为边的菱形OABC的顶点C在x轴的正半轴上,把菱形OABC沿AB向上翻折得到菱形ABDE.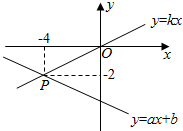 如图,已知直线y=ax+b和直线y=kx交于点P(-4,-2),则关于x,y的二元一次方程组$\left\{\begin{array}{l}y=ax+b\\ y=kx\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$.
如图,已知直线y=ax+b和直线y=kx交于点P(-4,-2),则关于x,y的二元一次方程组$\left\{\begin{array}{l}y=ax+b\\ y=kx\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$.