题目内容
14. 如图,在△ABC中,∠C=90°,∠B=30°,D为AB上一点,DE⊥BC于E.若BE=AC,DE+BC=3,求BD的长.
如图,在△ABC中,∠C=90°,∠B=30°,D为AB上一点,DE⊥BC于E.若BE=AC,DE+BC=3,求BD的长.
分析 设DE=x,则BD=2x,BE=$\sqrt{3}$x,所以AC=$\sqrt{3}$x,再在Rt△ACB利用正切的定义可表示出BC=3x,由于DE+BC=3,则x+3x=3,解得x=$\frac{3}{4}$,所以BD=2x=$\frac{3}{2}$.
解答 解:∵∠C=90°,∠B=30°,
设DE=x,则BD=2x,BE=$\sqrt{3}$x,
∵BE=AC,∴AC=$\sqrt{3}$x,
∵DE⊥BC,
∴∠ACB=90°,
在Rt△ACB,∵tanB=$\frac{AC}{BC}$=$\frac{\sqrt{3}}{3}$,
∴BC=$\frac{\sqrt{3}x}{tan30°}$=3x,
而DE+BC=3,
∴x+3x=3,解得x=$\frac{3}{4}$,
∴BD=2x=$\frac{3}{2}$.
点评 本题考查了解直角三角形,含30°角的直角三角形的性质,根据题意列方程是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.对于抛物线y=-$\frac{1}{3}$(x-5)2+3,下列说法正确的是( )
| A. | 开口向上 | B. | 顶点坐标(-5,3) | ||
| C. | 与y轴的交点坐标是(0,3) | D. | 当x>5时,y随x的增大而减小 |
5.某种动物活到20岁的概率为0.6,活到25岁的概率为0.4,则现年20岁的这种动物活到25岁的概率为( )
| A. | 0.24 | B. | 0.4 | C. | 0.6 | D. | $\frac{2}{3}$ |
9.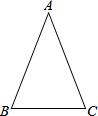 如图,△ABC中,AB=AC=13cm,BC=10cm.则△ABC内切圆的半径是( )
如图,△ABC中,AB=AC=13cm,BC=10cm.则△ABC内切圆的半径是( )
 如图,△ABC中,AB=AC=13cm,BC=10cm.则△ABC内切圆的半径是( )
如图,△ABC中,AB=AC=13cm,BC=10cm.则△ABC内切圆的半径是( )| A. | $\frac{10}{3}$ | B. | $\frac{13}{2}$ | C. | 4 | D. | 5 |
17.一个六棱柱的顶点个数、棱的条数、面的个数分别是( )
| A. | 6、12、6 | B. | 12、18、8 | C. | 18、12、6 | D. | 18、18、24 |
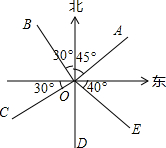 如图.根据点A、B、C、D、E在图中的位置填空.
如图.根据点A、B、C、D、E在图中的位置填空.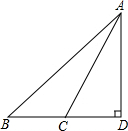 如图,Rt△ABC中,∠D=90°,∠B=45°,∠ACD=60°,BC=10cm,求AD的长.
如图,Rt△ABC中,∠D=90°,∠B=45°,∠ACD=60°,BC=10cm,求AD的长.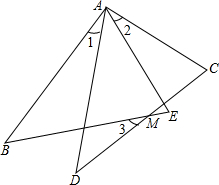 如图所示,AB=AD,AC=AE,∠1=∠2,猜想∠1与∠3的大小关系,并说明你猜想的正确性.
如图所示,AB=AD,AC=AE,∠1=∠2,猜想∠1与∠3的大小关系,并说明你猜想的正确性.