题目内容
1.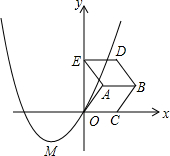 如图,在平面直角坐标系中,过原点的抛物线的顶点M的坐标为(-1,-1),点A的坐标为(1,1),以OA为边的菱形OABC的顶点C在x轴的正半轴上,把菱形OABC沿AB向上翻折得到菱形ABDE.
如图,在平面直角坐标系中,过原点的抛物线的顶点M的坐标为(-1,-1),点A的坐标为(1,1),以OA为边的菱形OABC的顶点C在x轴的正半轴上,把菱形OABC沿AB向上翻折得到菱形ABDE.(1)求抛物线对应的函数关系式;
(2)若把抛物线向右平移使抛物线经过点D,求平移的距离.
分析 (1)设抛物线解析式为顶点式y=a(x+1)2-1(a≠0).然后把原点的坐标代入即可求得系数a的值;
(2)如图所示,过点A作AP⊥x轴于点P.根据坐标与图形的性质、菱形的性质以及勾股定理易得点D的坐标是($\sqrt{2}$,2),把y=2代入函数解析式y=(x+1)2-1即可求得相应的x的值,所以结合点D的坐标即可得到平移的距离.
解答 解:(1)设抛物线解析式为y=a(x+1)2-1(a≠0).
把(0,0)代入,得
0=a(0+1)2-1,
解得a=1.
所以该抛物线的解析式为:y=(x+1)2-1;
(2)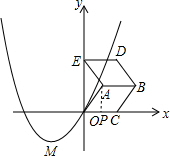 如图所示,过点A作AP⊥x轴于点P.
如图所示,过点A作AP⊥x轴于点P.
∵点A的坐标为(1,1),
∴OP=AP=1.
在直角△OAP中,由勾股定理得到:OA=$\sqrt{2}$.
∵四边形OABC为菱形,AB∥x轴.
∴OC=OA=$\sqrt{2}$.
∵把菱形OABC沿AB向上翻折得到菱形ABDE,
∴DE=OC=$\sqrt{2}$,DE∥x轴.
∴点D的坐标是($\sqrt{2}$,2),
由题意得:(x+1)2-1=2,
解得x1=$\sqrt{3}$-1,x2=-$\sqrt{3}$-1,
∴平移距离为:$\sqrt{2}$-$\sqrt{3}$+1或$\sqrt{2}$+$\sqrt{3}$+1.
点评 本题综合考查了待定系数法求二次函数解析式,菱形的性质,勾股定理以及二次函数图象的几何变换.解答(1)题时,要熟悉二次函数解析式的三种形式,并结合题中已知条件来设抛物线的解析式;解答(2)题时,要注意确定平移的距离为两种情况:抛物线对称轴的左侧经过点D、抛物线对称轴的右侧经过点D.

练习册系列答案
相关题目
18.李婷是一位运动鞋经销商,为了解鞋子的销售情况,随机调查了9位学生的鞋子的尺码,由小到大是:20,21,21,22,22,22,22,23,23.对这组数据的分析中,李婷最感兴趣的数据代表是( )
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
6. 数x、y在数轴上对应点如图所示,则化简|x+y|-|y-x|的结果是( )
数x、y在数轴上对应点如图所示,则化简|x+y|-|y-x|的结果是( )
 数x、y在数轴上对应点如图所示,则化简|x+y|-|y-x|的结果是( )
数x、y在数轴上对应点如图所示,则化简|x+y|-|y-x|的结果是( )| A. | 0 | B. | 2x | C. | 2y | D. | 2x-2y |
11.下列函数中,不是反比例函数的是( )
| A. | y=5x-1 | B. | y=$\frac{x}{5}$ | C. | y=$\frac{5}{x}$ | D. | xy=5 |
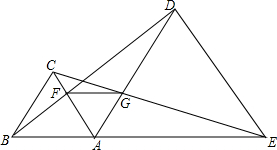 如图,点B、A、E在同一条直线上,△ABC和△ADE是这条直线上方的两个正三角形,连结BD、CE分别交AC、AD于点F、G,连结FG.求证:△AFG是正三角形.
如图,点B、A、E在同一条直线上,△ABC和△ADE是这条直线上方的两个正三角形,连结BD、CE分别交AC、AD于点F、G,连结FG.求证:△AFG是正三角形.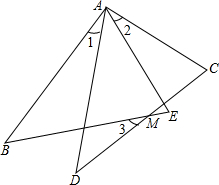 如图所示,AB=AD,AC=AE,∠1=∠2,猜想∠1与∠3的大小关系,并说明你猜想的正确性.
如图所示,AB=AD,AC=AE,∠1=∠2,猜想∠1与∠3的大小关系,并说明你猜想的正确性.