题目内容
8.当x,y为何值时,代数式x2+y2-4x+6y+19有最小值?并求出最小值.分析 将原式中19拆成4+9+6,使4、9与前面四项构成完全平方式,再根据非负数性质即可得最小值情况.
解答 解:∵x2+y2-4x+6y+19
=x2-4x+4+y2+6y+9+6
=(x-2)2+(y+3)2+6,
∴当x-2=0,y+3=0,即x=2,y=-3时有最小值,最小值为6
∴当x=2,y=-3时,多项式的最小值为6.
点评 此题考查了因式分解-运用公式法,以及非负数的性质,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
相关题目
19.有五张彩纸(形状、大小、质地都相同),茗茗在上面分别写下了5个不同的字母,分别是B,N,S,T,O,将彩纸背面朝上洗匀,从中抽取一张彩纸,正面的字母一定满足既是轴对称图形,又是中心对称图形的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
 如图,在?ABCD中,点F在边AD上,BF交AC于点E,过点E作EG∥BC交AB于点G,若AF:FD=2:1,求GE:BC的值.
如图,在?ABCD中,点F在边AD上,BF交AC于点E,过点E作EG∥BC交AB于点G,若AF:FD=2:1,求GE:BC的值.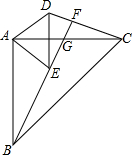 如图,已知AB=AC,AD=AE,∠BAC=90°,∠EAD=90°,BE的延长线交AC于G,交CD于F.
如图,已知AB=AC,AD=AE,∠BAC=90°,∠EAD=90°,BE的延长线交AC于G,交CD于F.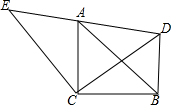 如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边上,连接BD.
如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边上,连接BD.