题目内容
20.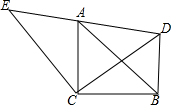 如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边上,连接BD.
如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边上,连接BD.(1)试判断△ACE与△BCD是否全等(不要求证明);
(2)求∠ADB的度数;
(3)求证:AE2+AD2=2AC2.
分析 (1)根据等腰直角三角形的性质得CE=CD,CA=CB,∠ECD=∠ACB,由此即可证明.
(2)由△ECA≌△DCA得∠EAC=∠CBD,因为∠EAC+∠CAD=180°,所以∠CAD+∠CBD=180°,由此可以证明∠ACB+∠ADB=180°,再根据等腰三角形的性质可以解决问题.
(3)由(1)可知AE=BD,在RT△ADB中利用勾股定理即可解决.
解答 (1)解:结论△ACE≌△BCD,
理由:∵△ACB和△ECD都是等腰直角三角形,
∴CE=CD,CA=CB,∠ECD=∠ACB=90°,
∴∠ECA=∠DCB,
在△ACE和△BCD中,
$\left\{\begin{array}{l}{CE=CD}\\{∠ECA=∠DCB}\\{AC=CB}\end{array}\right.$,
∴△ECA≌△DCA.
(2)解:∵△ACE≌△BCD,
∴∠EAC=∠CBD,
∵∠EAC+∠CAD=180°,
∴∠CAD+∠CBD=180°,
∴∠ACB+∠ADB=180°,
∵∠ACB=90°,
∴∠ADB=90°,
∵∠E=∠EDC=45°,
∴∠BDC=45°.
(3)证明:∵△ACE≌△BCD,
∴BD=AE,
由(2)可知∠ADB=90°,
∴AD2+BD2=AB2,
∵AC=BC,∠ACB=90°,
∴AB=$\sqrt{2}$AC,
∴AE2+AD2=2AC2.
点评 本题考查全等三角形的判定和性质、勾股定理、等腰直角三角形的性质,寻找全等三角形是解题的关键,本题还用到四边形内角和定理,属于中考常考题型.

练习册系列答案
相关题目
8.下列各式成立的是( )
| A. | $\sqrt{{{({-2})}^2}}=-2$ | B. | $\sqrt{x^2}=x$ | C. | $\sqrt{{{({-6})}^2}}=6$ | D. | $\sqrt{4\frac{1}{3}}=\frac{2}{3}\sqrt{3}$ |
5.下列命题中,假命题是( )
| A. | 在同圆中,相等的弧所对的弦相等 | |
| B. | 在同圆中,相等的弦所对的弧相等 | |
| C. | 在同圆中,相等的弧所对的圆心角相等 | |
| D. | 在同圆中,相等的圆心角所对的弦相等 |
12.如果三角形的两条边分别为8和6,那么连接该三角形三边中点所得的周长可能是下列数据中的( )
| A. | 8 | B. | 10 | C. | 14 | D. | 16 |
10.下列计算正确的是( )
| A. | (a-b)2=a2-b2 | B. | (-2a2)3=8a6 | C. | 2a2+a2=3a2 | D. | a3÷a=a3 |
 已知实数a,b,c在数轴上的位置如图所示,且|a|=|b|,化简:|a|+|a+b|-$\sqrt{(c-a)^{2}}$-2$\sqrt{{c}^{2}}$=3c-2a.
已知实数a,b,c在数轴上的位置如图所示,且|a|=|b|,化简:|a|+|a+b|-$\sqrt{(c-a)^{2}}$-2$\sqrt{{c}^{2}}$=3c-2a. 如图,已知△ABC∽△AED,若∠C=60°,∠B=70°,则∠DEA=70°.
如图,已知△ABC∽△AED,若∠C=60°,∠B=70°,则∠DEA=70°.