题目内容
19.如图所示,直线l为等边三角形△ABC经过点A的一条对称轴,直线l交BC于点M,动点D在直线l上运动,以CD为一边在CD的下方作等边三角形△CDE,连接BE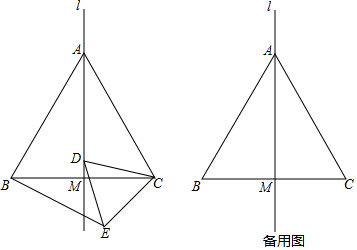
(1)填空∠CAM=30°.
(2)当点D在线段AM上运动时(点D与点A、M不重合),试说明△ACD≌△BCE;
(3)当点D在线段AM的延长线上运动时,AD=BE吗?请说明理由.
分析 (1)根据等边三角形过一顶点的对称轴平分该角,可得结果;
(2)根据等边三角形的性质可利用SAS证明两三角形全等;
(3)同理证明△ACD≌△BCE可得结果.
解答 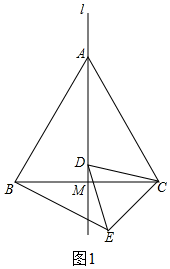 解:(1)∵直线l为等边三角形△ABC经过点A的一条对称轴,
解:(1)∵直线l为等边三角形△ABC经过点A的一条对称轴,
∴AM平分∠BAC,
∴∠CAM=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×60°=30°,
故答案为:30°;
(2)如图1,D在线段AM上,
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∵△DCE是等边三角形,
∴DC=EC,∠DCE=60°,
∴∠ACB=∠DCE,
∴∠ACB-∠DCB=∠DCE-∠DCB,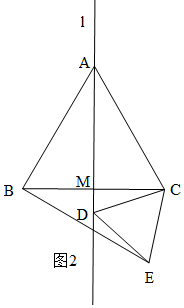
即∠ACD=∠BCE,
在△ACD和△BCE中,
∵$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{DC=EC}\end{array}\right.$,
∴△ACD≌△BCE(SAS);
(3)当点D在线段AM的延长线上运动时,AD=BE,理由是:
如图2,D在线段AM的延长线上,
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∵△DCE是等边三角形,
∴DC=EC,∠DCE=60°,
∴∠ACB=∠DCE,
∴∠ACB+∠DCB=∠DCE+∠DCB
即∠ACD=∠BCE,
在△ACD和△BCE中,
∵$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{DC=EC}\end{array}\right.$,
∴△ACD≌△BCE(SAS);
∴AD=BE.
点评 本题考查了等边三角形的性质、三角形全等的性质和判定,知道等边三角形是轴对称图形,并熟练掌握三角形全等的判定方法.

练习册系列答案
相关题目
14.已知三角形的两边长分别是2和5,则下列线段可能是此三角形的第三边的是( )
| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
4.下列各组数中,互为相反数的一组是( )
| A. | -(-8)与+(+8) | B. | -(+8)与-|-8| | C. | -|-8|与+(-8) | D. | -22与(-2)2 |
11.根据下列表述,能确定位置的是( )
| A. | 东经118°,北纬40° | B. | 南京市白下路 | ||
| C. | 北偏东30° | D. | 红星电影院第2排 |
8.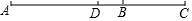 如图,已知线段AB=9,BC=5,点D为线段AC的中点,则线段AD的长度是( )
如图,已知线段AB=9,BC=5,点D为线段AC的中点,则线段AD的长度是( )
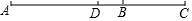 如图,已知线段AB=9,BC=5,点D为线段AC的中点,则线段AD的长度是( )
如图,已知线段AB=9,BC=5,点D为线段AC的中点,则线段AD的长度是( )| A. | 2 | B. | 2.5 | C. | 4.5 | D. | 7 |
 (1)比较大小:$\sqrt{5}$+1>$\sqrt{10}$(填“>”、“<”或者“=”);
(1)比较大小:$\sqrt{5}$+1>$\sqrt{10}$(填“>”、“<”或者“=”);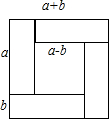 阅读下面材料:
阅读下面材料: