题目内容
9.如图,在同一平面内∠ABC=45°,过点B的直线l⊥BC,点P为直线l上一动点.(1)如图,连接PC交AB于点Q,若BP=2,BC=3,求$\frac{PQ}{CQ}$的值;
(2)如图,连接PC交AB于点Q,过点B作BD⊥PC于点D,当∠BPC=3∠C时,试判断线段BD与线段CQ的数量关系,并证明你的结论.
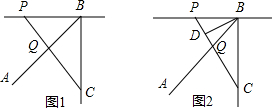
分析 (1)如图1,过C作CE⊥BC交AB于E,由∠ABC=45°,于是得到△BCE是等腰直角三角形,根据等腰直角三角形的性质得到CE=BC=3,推出△BPQ∽△ECQ,根据相似三角形的性质即可得到结论;
(2)如图2,过C作CH⊥AB交BD的延长线于H,交AB于G,由∠ABC=45°,得到△BCG是等腰直角三角形,由等腰直角三角形的性质得到∠BCH=45°,BG=CG,由∠BPC=3∠BCP,∠BCP+∠BPC=90°,于是得到∠BCP=22.5°,推出∠HCP=∠BCH-∠BCP=22,5°=∠BCP,于是得到△BCH是等腰三角形,根据等腰三角形的性质得到BD=DH=$\frac{1}{2}$BH,即BH=2BD,推出∠HDQ=∠HGQ=90°,求得∠H+∠DQG=∠CQG+∠DQG=180°,得到∠H=∠CQG,根据全等三角形的性质得到CQ=BH,即可得到结论.
解答 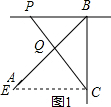 解:(1)如图1,过C作CE⊥BC交AB于E,
解:(1)如图1,过C作CE⊥BC交AB于E,
∵∠ABC=45°,
∴△BCE是等腰直角三角形,
∴CE=BC=3,
∵PB⊥BC,
∴PB∥CE,
∴△BPQ∽△ECQ,
∴$\frac{PQ}{CQ}=\frac{PB}{CE}=\frac{2}{3}$;
(2)如图2,过C作CH⊥AB交BD的延长线于H,交AB于G,
∵∠ABC=45°,
∴△BCG是等腰直角三角形,
∴∠BCH=45°,BG=CG,
∵∠BPC=3∠BCP,
∵∠BCP+∠BPC=90°,
∴∠BCP=22.5°,
∴∠HCP=∠BCH-∠BCP=22,5°=∠BCP,
∵BH⊥PC,
∴△BCH是等腰三角形,
∴BD=DH=$\frac{1}{2}$BH,即BH=2BD,
∴∠HDQ=∠HGQ=90°,
∴∠H+∠DQG=∠CQG+∠DQG=180°,
∴∠H=∠CQG,
在△BGH与△CQG中,
$\left\{\begin{array}{l}{∠H=∠CQG}\\{∠BGH=∠QGC}\\{BG=CG}\end{array}\right.$,
∴△BGH≌△CGQ,
∴CQ=BH,
∴CQ=2BD.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,角平分线的定义,等腰三角形的性质,正确的作出辅助线是解题的关键.

| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
| A. | $\overrightarrow{a}$-$\overrightarrow{b}$=0 | B. | $\overrightarrow{a}$-$\overrightarrow{b}$=$\overrightarrow{b}$-$\overrightarrow{a}$ | ||
| C. | 如果$\overrightarrow{a}$=$\overrightarrow{b}$,那么|$\overrightarrow{a}$|=|$\overrightarrow{b}$| | D. | 如果|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,那么$\overrightarrow{a}$=$\overrightarrow{b}$. |
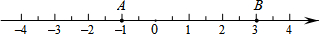
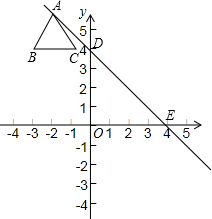 在平面直角坐标系中,直线y=kx+b经过两点D(0,4),E(4,0),边长为2个单位长度的等边△ABC,顶点A在该直线上滑动,在滑动过程中始终保持边BC∥x轴,且顶点A在BC的上方.
在平面直角坐标系中,直线y=kx+b经过两点D(0,4),E(4,0),边长为2个单位长度的等边△ABC,顶点A在该直线上滑动,在滑动过程中始终保持边BC∥x轴,且顶点A在BC的上方.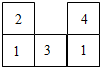 图中是由几个小立方块搭成的几何体的从上面看的形状图,小正方形中的数字表示在该位置的小立方块的个数,请画出这个几何体的从正面看和从左面看的形状图.
图中是由几个小立方块搭成的几何体的从上面看的形状图,小正方形中的数字表示在该位置的小立方块的个数,请画出这个几何体的从正面看和从左面看的形状图.