题目内容
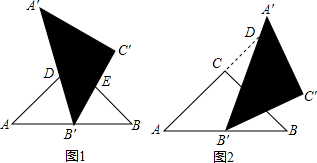
2.现有两块等腰直角形三角板,如图,把其中一块三角板A′B′C′的一个锐角顶点B'放在另一块三角板ABC斜边AB的中点处,并使三角板A′B′C′绕着点B′旋转.(1)当两块三角板相对位置如图①,即AC与A′B′交于点D,BC与B′C′交于点E时,求证:△AB′D∽△BEB′:
(2)当两块三角板相对位置如图②,即AC边的延长线与A′B′交于点D,BC与B′C′交于点E时,△AB′D与△BEB′还相似吗?(直接给出结论.不需证明)
(3)在图②中,连结DE,试探究△AB′D与△B′ED是否相似,并说明理由或给出证明.
(4)在图①中,若△ABC改为角C等于150°的等腰三角形,那么△A′B′C′只要满足∠A′B′C′=15°时,仍有△AB′D∽△BEB′.
分析 (1)根据题意可知∠A=∠B=45°,然后根据∠ADB′+∠A=∠A′B′C′+∠EB′B,从而可证明:∠ADB′=∠EB′B,从而可证明两三角形相似;
(2)根据(1)的思路证明:∠A=∠B,∠ADB′=∠EB′B,从而可证明两三角形相似;
(3)由(2)可知△AB′D∽△BEB′,根据相似三角形的性质可知$\frac{AD}{BB′}=\frac{B′D}{EB′}$,因为BB′=AB′,从而可得到$\frac{AD}{AB′}=\frac{B′D}{B′E}$,又因为∠A=∠A′B′C′=45°,从而可证明△AB′D∽△B′ED;
(4)当∠A′B′C′=15°时,可证明∠ADB′=∠EB′B,∠A=∠B,从而可证明两三角形相似.
解答 证明:(1)由等腰直角三角形的性质可知:∠A=∠B=∠A′B′C′=45°,
∵∠BB′D=∠ADB′+∠A,∠BB′D=∠A′B′C′+∠EB′B,
∴∠ADB′=∠BB′D-∠A=∠BB′D-45°,∠EB′B=∠BB′D-∠A′B′C′=∠BB′D-45°.
∴∠ADB′=∠EB′B.
又∵∠A=∠B,
∴△AB′D∽△BEB′.
(2)相似.
如下图: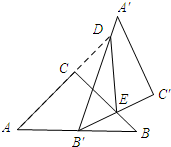
理由:由等腰直角三角形的性质可知:∠A=∠B=∠A′B′C′=45°,
∵∠BB′D=∠ADB′+∠A,∠BB′D=∠A′B′C′+∠EB′B,
∴∠ADB′=∠BB′D-∠A=∠BB′D-45°,∠EB′B=∠BB′D-∠A′B′C′=∠BB′D-45°.
∴∠ADB′=∠EB′B.
又∵∠A=∠B,
∴△AB′D∽△BEB′.
(3)由(2)可知
∴△AB′D∽△BEB′,
∴$\frac{AD}{BB′}=\frac{B′D}{EB′}$,
又∵BB′=AB′,
∴$\frac{AD}{AB′}=\frac{B′D}{B′E}$,
又∵∠A=∠A′B′C′=45°.
∴△AB′D∽△B′ED.
(4)当∠A′B′C′=15°时,△AB′D∽△BEB′.
理由:∵∠C=150°,AC=BC,
∴∠A=∠B=15°.
∵∠BB′D=∠ADB′+∠A,∠BB′D=∠A′B′C′+∠EB′B,
∴∠ADB′=∠BB′D-∠A=∠BB′D-15°,∠EB′B=∠BB′D-∠A′B′C′=∠BB′D-15°.
∴∠ADB′=∠EB′B.
又∵∠A=∠B,
∴△AB′D∽△BEB′.
点评 本题主要考查的是相似三角形的性质和判定,利用三角形外角的性质和等腰三角形的性质证得∠ADB′=∠EB′B是解题的关键.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案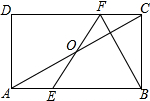 如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )| A. | 8$\sqrt{3}$ | B. | 8 | C. | 4$\sqrt{3}$ | D. | 6 |
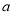 的正方形中挖掉一个边长为
的正方形中挖掉一个边长为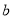 的小正方形(
的小正方形(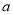 >
> 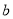 ),把余下部分剪拼成一个矩形(如图②),通过计算两个图形的面积,验证了一个等式,则这个等式是( )
),把余下部分剪拼成一个矩形(如图②),通过计算两个图形的面积,验证了一个等式,则这个等式是( )
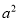 +ab-2
+ab-2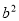
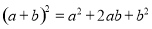
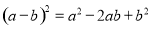
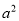 -
-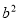 =(a+b)(a-b)
=(a+b)(a-b)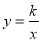 的图象相交于A(4,2)、B(-2,m)两点.则一次函数的表达式为________.
的图象相交于A(4,2)、B(-2,m)两点.则一次函数的表达式为________.