题目内容
10．
如图，矩形ABCD的边BC=6，且BC在平面直角坐标系中x轴的正半轴上，点B在点C的左侧，直线y=kx经过点A（3，3）和点P，且OP=6$\sqrt{2}$．将直线y=kx沿y轴向下平移得到直线y=kx+b，若点P落在矩形ABCD的内部，则b的取值范围是（ ）| A． | 0＜b＜3 | B． | -3＜b＜0 | C． | -6＜b＜-3 | D． | -3＜b＜3 |
分析 作PE⊥AD于E交BC于F，先求出直线y=kx以及点P坐标，再确定点E、F坐标，代入y=x+b中即可解决问题．
解答 解：如图作PE⊥AD于E交BC于F，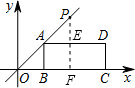
∵直线y=kx经过点A（3，3），
∴k=1，
∴直线为y=x，设点P坐标（a，a），
∵OP=6$\sqrt{2}$，
∴a2+a2=72，
∴a2=36，
∵a＞0，
∴a=6．
∴点P坐标（6，6），点E（6，3），点F（6，0），
把点E（6，3），点F（6，0）分别代入y=x+b中，得到b=-3或-6，
∴点P落在矩形ABCD的内部，
∴-6＜b＜-3．
故选C．
点评 本题考查一次函数有关知识，掌握两条直线平行k值相同，寻找特殊点是解决问题的关键，理解点P在平移过程中与y轴的距离保持不变，属于中考常考题型．
练习册系列答案
相关题目
1．
如图，在直角坐标系中，弹性小球从点P（0，3）出发，沿所示方向运动，每当小球碰到矩形OABC的边时反弹，反弹时，反射角等于入射角，当小球第1次碰到矩形的边时的点为P1，第2次碰到矩形的边时的点为P2，…，第n次碰到矩形的边时的点为Pn，则点P2016的坐标是（ ）
如图，在直角坐标系中，弹性小球从点P（0，3）出发，沿所示方向运动，每当小球碰到矩形OABC的边时反弹，反弹时，反射角等于入射角，当小球第1次碰到矩形的边时的点为P1，第2次碰到矩形的边时的点为P2，…，第n次碰到矩形的边时的点为Pn，则点P2016的坐标是（ ）| A． | （0，3） | B． | （5，0） | C． | （0，5） | D． | （7，4） |
18．
如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1、O2、O3，…组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒$\frac{π}{2}$个单位长度，则第2017秒时，点P的坐标是（ ）
如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1、O2、O3，…组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒$\frac{π}{2}$个单位长度，则第2017秒时，点P的坐标是（ ）| A． | （2016，0） | B． | （2017，1） | C． | （2017，-1） | D． | （2018，0） |
5．a、b都是实数，且a＜b，则下列不等式的变形正确的是（ ）
| A． | ac＜bc | B． | a+x＞b+x | C． | -a＞-b | D． | $\frac{a}{c}＜\frac{b}{c}$ |
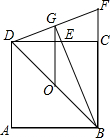如图，O是正方形ABCD的中心，BE平分∠DBC，交DC于点E，将点E绕着点C按顺时针方向旋转90°得到点F，连接CF，DF，BE的延长线交DF于点G，连接OG．
19．
二次函数y=a（x+m）2+n的图象如图，则一次函数y=mx+n的图象经过（ ）
二次函数y=a（x+m）2+n的图象如图，则一次函数y=mx+n的图象经过（ ）| A． | 二、三、四象限 | B． | 一、二、四象限 | C． | 一、三、四象限 | D． | 一、二、三象限 |