题目内容
9.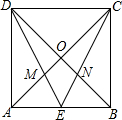 已知正方形ABCD的边长为1,对角线AC,BD交于点O,E为AB的中点,DE与AC交于点M,CE交BD于点N,则四边形OMEN的内切圆的半径等于$\frac{\sqrt{5}-\sqrt{2}}{6}$.
已知正方形ABCD的边长为1,对角线AC,BD交于点O,E为AB的中点,DE与AC交于点M,CE交BD于点N,则四边形OMEN的内切圆的半径等于$\frac{\sqrt{5}-\sqrt{2}}{6}$.
分析 利用面积转化S=r$•\frac{c}{2}$,由相似可得AM=$\frac{AC}{3}$,ME=$\frac{DE}{3}$,利用勾股定理可得AC,DE的长,从而得出四边形MENO的周长,由OM与OA的比例关系,易得△AOE的面积与△OME的面积比,可得△OME的面积,得四边形MENO的面积,根据周长与面积的关系得r.
解答 解:∵四边形ABCD为正方形,E为AB的中点,
∴AB∥CD,
∴△AME∽△CMD,
∵E为AB的中点,
∴$\frac{AE}{CD}=\frac{AM}{CM}=\frac{ME}{MD}$=$\frac{1}{2}$,
∴$\frac{AM}{AC}=\frac{1}{3}$,$\frac{ME}{DE}=\frac{1}{3}$,
∵AD=DC=1,
∴AE=$\frac{1}{2}$,
∴DE=$\frac{\sqrt{5}}{2}$,AC=$\sqrt{2}$,
∴ME=$\frac{\sqrt{5}}{6}$,AM=$\frac{\sqrt{2}}{3}$,
∴MO=AO-AM=$\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{3}$=$\frac{\sqrt{2}}{6}$,
∴四边形MENO的周长为:2×($\frac{\sqrt{5}}{6}+\frac{\sqrt{2}}{6}$)=$\frac{\sqrt{5}+\sqrt{2}}{3}$,
∵S四边形MENO=2S△MEO,
∵$\frac{{S}_{△MEO}}{{S}_{△AEO}}$=$\frac{OM}{OA}$=$\frac{1}{3}$,S△AEO=$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}$=$\frac{1}{8}$,
∴S△MEO=$\frac{1}{24}$,
∴S四边形MENO=$\frac{1}{12}$,
∴r=$\frac{1}{12}÷$($\frac{1}{2}$×$\frac{\sqrt{5}+\sqrt{2}}{3}$)=$\frac{\sqrt{5}-\sqrt{2}}{6}$,
故答案为:$\frac{\sqrt{5}-\sqrt{2}}{6}$.
点评 本题主要考查了多边形与其内切圆的关系,利用面积与周长的关系解得内切圆的半径是解答此题的关键.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案| A. | 12 | B. | 11 | C. | 14 | D. | 17 |
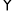 ABCD与
ABCD与 DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为_________°.
DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为_________°.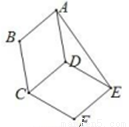
 用科学记数法表示为______________.
用科学记数法表示为______________.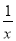 )
) 如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为60度.
如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为60度.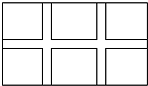 学校课外生物小组的试验园地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为600平方米,求小道的宽.
学校课外生物小组的试验园地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为600平方米,求小道的宽.