题目内容
1.因式分解:①-x2-4y2+4xy
②(a-1)x2+4(1-a)
分析 ①原式提取-1,再利用完全平方公式分解即可;
②原式变形后,提取公因式,再利用平方差公式分解即可.
解答 解:①原式=-(x2+4y2-4xy)=-(x-2y)2;
②原式=(a-1)x2-4(a-1)=(a-1)(x2-4)=(a-1)(x+2)(x-2).
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
16.下列运算正确的是( )
| A. | a2•a4=a8 | B. | 2a2+a2=3a4 | C. | 5a+3b=8ab | D. | (ab2)3=a3b6 |
6.计算(-2)100+(-2)99的结果是( )
| A. | 2 | B. | -2 | C. | -299 | D. | 299 |
13.要使$\sqrt{2x-4}$有意义,则( )
| A. | x≥2 | B. | x≤2 | C. | x<2 | D. | x>-2 |
10.一元二次方程(x-2)2=0的解为( )
| A. | x1=2,x2=-2 | B. | x1=x2=2 | C. | x=-2 | D. | x1=2,x2=0 |
 的值为1.
的值为1.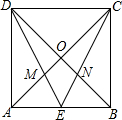 已知正方形ABCD的边长为1,对角线AC,BD交于点O,E为AB的中点,DE与AC交于点M,CE交BD于点N,则四边形OMEN的内切圆的半径等于$\frac{\sqrt{5}-\sqrt{2}}{6}$.
已知正方形ABCD的边长为1,对角线AC,BD交于点O,E为AB的中点,DE与AC交于点M,CE交BD于点N,则四边形OMEN的内切圆的半径等于$\frac{\sqrt{5}-\sqrt{2}}{6}$.