题目内容
18.已知$\sqrt{18-n}$是正整数,则实数n的最大值为( )| A. | 12 | B. | 11 | C. | 14 | D. | 17 |
分析 根据二次根式的定义得到18-n≥0,根据最小的正整数为1得到答案.
解答 解:由题意可知18-n是一个完全平方数,且不为0,最小为1,
所以n的最大值为18-1=17,
故选:D.
点评 主要考查了二次根式的定义,掌握二次根式的被开方数是非负数和完全平方数的概念是解题的关键.

练习册系列答案
相关题目
6.计算(-2)100+(-2)99的结果是( )
| A. | 2 | B. | -2 | C. | -299 | D. | 299 |
13.要使$\sqrt{2x-4}$有意义,则( )
| A. | x≥2 | B. | x≤2 | C. | x<2 | D. | x>-2 |
10.一元二次方程(x-2)2=0的解为( )
| A. | x1=2,x2=-2 | B. | x1=x2=2 | C. | x=-2 | D. | x1=2,x2=0 |
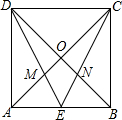 已知正方形ABCD的边长为1,对角线AC,BD交于点O,E为AB的中点,DE与AC交于点M,CE交BD于点N,则四边形OMEN的内切圆的半径等于$\frac{\sqrt{5}-\sqrt{2}}{6}$.
已知正方形ABCD的边长为1,对角线AC,BD交于点O,E为AB的中点,DE与AC交于点M,CE交BD于点N,则四边形OMEN的内切圆的半径等于$\frac{\sqrt{5}-\sqrt{2}}{6}$.